Giải bài tập 5.27 trang 107 SGK Toán 9 tập 1 - Kết nối tri thức
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A. Một đường thẳng qua A cắt (O) tại B và cắt (O’) tại C. Chứng minh rằng OB // O’C.
Đề bài
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A. Một đường thẳng qua A cắt (O) tại B và cắt (O’) tại C. Chứng minh rằng OB // O’C.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất của tam giác cân và hai góc đối đỉnh suy ra \(\widehat {{\rm{OBA}}} = \widehat {{\rm{O'CA}}}\)
Khi đó OB // O’C.
Lời giải chi tiết
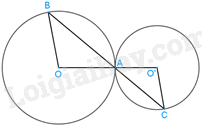
Vì OA = OB nên tam giác OAB cân tại O.
Suy ra: \(\widehat {{\rm{OBA}}} = \widehat {{\rm{OAB}}}\)
Vì O’A = O’C nên tam giác O’AC cân tại O.
Suy ra: \(\widehat {{\rm{O'AC}}} = \widehat {{\rm{O'CA}}}\)
Lại có: \(\widehat {{\rm{OAB}}} = \widehat {{\rm{O'AB}}}\)
Suy ra: \(\widehat {{\rm{OBA}}} = \widehat {{\rm{O'CA}}}\)
Vậy OB // O’C.
Cùng chủ đề:
Giải bài tập 5. 27 trang 107 SGK Toán 9 tập 1 - Kết nối tri thức