Giải bài tập 9.36 trang 91 SGK Toán 9 tập 2 - Kết nối tri thức
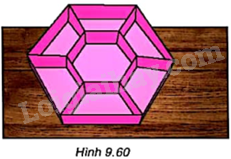
Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10cm và chia thành 7 ngăn gồm một lục giác đều nhỏ và 6 hình thang cân như Hình 9.60. Hỏi lục giác đều nhỏ phải có cạnh bằng bao nhiêu để nó có diện tích bằng hai lần diện tích mỗi hình thang?
Đề bài
Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10cm và chia thành 7 ngăn gồm một lục giác đều nhỏ và 6 hình thang cân như Hình 9.60. Hỏi lục giác đều nhỏ phải có cạnh bằng bao nhiêu để nó có diện tích bằng hai lần diện tích mỗi hình thang?
Phương pháp giải - Xem chi tiết
- Gọi O là tâm đa giác lớn và đa giác nhỏ.
- Dựa vào kiến thức về lục giác đều, ta có hình lục giác được chia thành 6 tam giác đều chung đỉnh O, 2 đỉnh còn lại là các đỉnh 2 đỉnh kề nhau của lục giác.
- Lấy hai điểm A, B là hai đỉnh kề nhau của lục giác nhỏ như hình vẽ. Đặt AB = x (cm). Khi đó ta có \(\Delta AOB\) đều.
- Kẻ \(OH \bot AB\), tính đường cao OH của tam giác AOB. Từ đó ta tính được \({S_{\Delta AOB}}\).
Từ đó ta tính được diện tích hình lục giác đều nhỏ: S lục giác đều nhỏ \( = 6.{S_{\Delta AOB}}\).
Vì diện tích lục giác đều nhỏ bằng hai lần diện tích mỗi hình thang nên diện tích mỗi hình thang là:
S hình thang = S lục giác đều nhỏ : 2, suy ra tổng diện tích 6 hình thang.
Ta tính được S lục giác đều lớn = S lục giác đều nhỏ + S 6 hình thang .
Mà ta còn tính được diện tích hình lục giác đều lớn qua cạnh của nó giống như S lục giác đều nhỏ .
Từ đó giải phương trình để tìm x.
Lời giải chi tiết
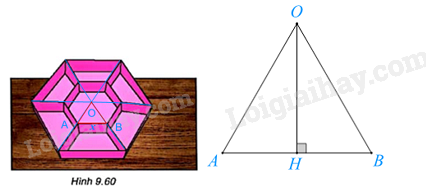
Nối các cặp đỉnh đối diện của lục giác với nhau, ta được điểm O là tâm của hình lục giác lớn và lục giác nhỏ.
Ta chia hình lục giác thành 6 tam giác đều chung đỉnh O, 2 đỉnh còn lại là các đỉnh 2 đỉnh kề nhau của lục giác.
Lấy hai điểm A, B là hai đỉnh kề nhau của lục giác nhỏ như hình vẽ. Đặt AB = x (cm) \(\left( {0 < x < 10} \right)\).
Khi đó \(\Delta AOB\) đều có \(OA = OB = AB = x\) và \(\widehat B = 60^\circ \).
Kẻ \(OH \bot AB\). Dựa vào hệ thức giữa cạnh và góc trong tam giác vuông, ta có:
\(OH = OB.\sin \widehat {OBA} = x.\sin 60^\circ = \frac{{\sqrt 3 }}{2}x\left( {cm} \right)\)
Suy ra \({S_{\Delta AOB}} = \frac{{OH.AB}}{2} = \frac{{\frac{{\sqrt 3 }}{2}x.x}}{2} = \frac{{{x^2}\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Ta có diện tích hình lục giác đều nhỏ là:
S lục giác đều nhỏ \( = 6.{S_{\Delta AOB}} = 6.\frac{{{x^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\).
Theo đề bài, diện tích lục giác đều nhỏ bằng hai lần diện tích mỗi hình thang nên diện tích mỗi hình thang là:
S hình thang = S lục giác đều nhỏ : 2 = \(\frac{{3\sqrt 3 {x^2}}}{2}:2 = \frac{{3\sqrt 3 {x^2}}}{4}\left( {c{m^2}} \right)\),
suy ra tổng diện tích 6 hình thang là: \(6.\frac{{3\sqrt 3 {x^2}}}{4} = \frac{{9\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\)
Do đó, diện tích lục giác đều lớn là:
S lục giác đều lớn = S lục giác đều nhỏ + S 6 hình thang \( = \frac{{3\sqrt 3 {x^2}}}{2} + \frac{{9\sqrt 3 {x^2}}}{2} = \frac{{12\sqrt 3 {x^2}}}{2} = 6\sqrt 3 {x^2}\left( {c{m^2}} \right)\) (1)
Mà tương tự như S lục giác đều nhỏ , ta cũng có thể tính được diện tích lục giác đều theo độ dài cạnh của nó theo công thức \(S = \frac{{3\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\) với x là độ dài cạnh.
Suy ra S lục giác đều lớn \( = \frac{{3\sqrt 3 {{.10}^2}}}{2} = 150\sqrt 3 \left( {c{m^2}} \right)\) (2)
Từ (1) và (2), ta có phương trình: \(6\sqrt 3 {x^2} = 150\sqrt 3 \)
suy ra \({x^2} = 25\), do đó \(x = 5\)(thỏa mãn vi \(0 < x < 10\)).
Vậy cạnh của lục giác đều nhỏ là 5cm.