Giải bài tập 9.40 trang 92 SGK Toán 9 tập 2 - Kết nối tri thức
Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC và I là trung điểm của AH. Chứng minh rằng: a) Tứ giác AEHF nội tiếp đường tròn tâm I; b) ME, MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.
Đề bài
Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC và I là trung điểm của AH. Chứng minh rằng:
a) Tứ giác AEHF nội tiếp đường tròn tâm I;
b) ME, MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.
Phương pháp giải - Xem chi tiết
a) + Chứng minh \(\widehat {AEH} = \widehat {AFH} = {90^o}\) nên tam giác AEH vuông tại E, tam giác AHF vuông tại F.
+ Suy ra, tứ giác AEHF nội tiếp đường tròn tâm I.
b) Chứng minh \(\widehat {IEA} = \widehat {EBC}\), \(\widehat {MCE} = \widehat {MEC}\), \(\widehat {ECB} + \widehat {EBC} = {90^o}\) nên \(\widehat {MEC} + \widehat {IEA} = {90^o}\).
+ Tính được \(\widehat {IEM} = {90^o}\) nên \(IE \bot ME\) tại M, nên ME tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.
+ Chứng minh tương tự ta có: MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.
Lời giải chi tiết
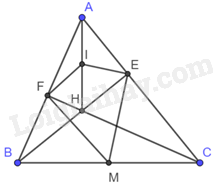
a) Vì BE, CF là đường cao của \(\Delta \)ABC nên \(BE \bot AC,CF \bot AB\)\( \Rightarrow \widehat {AEH} = \widehat {AFH} = \widehat {BFC} = \widehat {BEC} = {90^o}\)
Do đó, tam giác AFH vuông tại F và tam giác AEH vuông tại E.
Suy ra, bốn điểm A, E, H, F cùng thuộc đường tròn đường kính AH.
Mà I là trung điểm của AH nên tứ giác AEHF nội tiếp đường tròn tâm I.
b) Vì tứ giác AEHF nội tiếp đường tròn tâm I nên \(IA = IE\). Do đó, \(\Delta \)IAE cân tại I nên \(\widehat {IAE} = \widehat {IEA}\).
Lại có: \(\widehat {EAI} = \widehat {EBC}\) (cùng phụ với góc ACB) nên \(\widehat {IEA} = \widehat {EBC}\) (1)
\(\Delta \)BEC vuông tại E, EM là đường trung tuyến nên \(EM = MC\). Do đó, \(\Delta \)MEC cân tại M.
Suy ra, \(\widehat {MCE} = \widehat {MEC}\) (2)
\(\Delta \)BEC vuông tại E nên \(\widehat {ECB} + \widehat {EBC} = {90^o}\) (3)
Từ (1), (2) và (3) ta có: \(\widehat {MEC} + \widehat {IEA} = {90^o}\).
Mà \(\widehat {MEC} + \widehat {IEA} + \widehat {IEH} + \widehat {HEM} = {180^o} \Rightarrow \widehat {IEM} = {90^o}\). Do đó, \(IE \bot ME\) tại M. Mà E thuộc đường tròn ngoại tiếp tứ giác AEHF nên ME tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.
Chứng minh tương tự ta có: MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.