Giải bài tập 9.42 trang 92 SGK Toán 9 tập 2 - Kết nối tri thức
Cho một hình lục giác đều và một hình vuông cùng nội tiếp một đường tròn. Biết rằng hình vuông có cạnh bằng 3cm. Tính chu vi và diện tích của một hình lục giác đều đã cho.
Đề bài
Cho một hình lục giác đều và một hình vuông cùng nội tiếp một đường tròn. Biết rằng hình vuông có cạnh bằng 3cm. Tính chu vi và diện tích của một hình lục giác đều đã cho.
Phương pháp giải - Xem chi tiết
+ Gọi hình vuông ABCD và lục giác đều EFGHIJ cùng nội tiếp đường tròn (O).
+ Áp dụng định lí Pythagore vào tam giác ABC vuông tại B để tính AC, từ đó suy ra bán kính (O).
+ Chứng minh \(\Delta EOF = \Delta GOF = \Delta GOH = \Delta IOH = \Delta IOJ = \Delta EOJ\left( {c.c.c} \right)\), suy ra \(\widehat {EOF} = \widehat {FOG} = \widehat {GOH} = \widehat {HOI} = \widehat {IOJ} = \widehat {JOE} = \frac{{{{360}^o}}}{6} = {60^o}\)
+ Chứng minh tam giác EOF đều, từ đó tính được EF.
+ Chu vi lục giác đều EFGHIJ là: \(P = 6EF\).
+ Tính diện tích tam giác EOF.
+ Diện tích lục giác EFGHIJ bằng 6 lần diện tích tam giác EOF.
Lời giải chi tiết
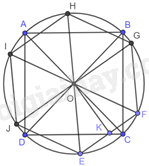
Gọi hình vuông ABCD và lục giác đều EFGHIJ cùng nội tiếp đường tròn (O).
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:
\(A{C^2} = A{B^2} + B{C^2} \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = 3\sqrt 2 \left( {cm} \right)\)
Do đó, bán kính đường tròn (O) bằng \(\frac{{3\sqrt 2 }}{2}cm\).
Vì EFGHIJ là lục giác đều \(EF = FG = GH = HI = IJ = JE\)
Mà lục giác EFGHIJ nội tiếp (O) nên \(OE = OF = OG = OH = OI = OJ\).
Do đó, \(\Delta EOF = \Delta GOF = \Delta GOH = \Delta IOH = \Delta IOJ = \Delta EOJ\left( {c.c.c} \right)\)
Suy ra, \(\widehat {EOF} = \widehat {FOG} = \widehat {GOH} = \widehat {HOI} = \widehat {IOJ} = \widehat {JOE} = \frac{{{{360}^o}}}{6} = {60^o}\)
Tam giác EOF có: \(OE = OF,\widehat {EOF} = {60^o}\) nên tam giác EOF đều.
Do đó, \(OE = EF = \frac{{3\sqrt 2 }}{2}cm\)
Chu vi lục giác đều EFGHIJ là: \(P = 6EF = 6.\frac{{3\sqrt 2 }}{2} = 9\sqrt 2 \left( {cm} \right)\)
Kẻ OK vuông góc với EF tại K. Khi đó, OK là đường trung tuyến trong tam giác đều EOF.
Suy ra: \(EK = \frac{1}{2}EF = \frac{{3\sqrt 2 }}{4}cm\)
Áp dụng định lí Pythagore vào tam giác OKE vuông tại K có:
\(O{K^2} + K{E^2} = O{E^2} \Rightarrow OK = \sqrt {O{E^2} - K{E^2}} = \frac{{3\sqrt 6 }}{4}\left( {cm} \right)\)
Diện tích tam giác EOF là:
\({S_{EOF}} = \frac{1}{2}OK.EF = \frac{1}{2}.\frac{{3\sqrt 6 }}{4}.\frac{{3\sqrt 2 }}{2} = \frac{{9\sqrt 3 }}{8}\left( {c{m^2}} \right)\)
Vì \(\Delta EOF = \Delta GOF = \Delta GOH = \Delta IOH = \Delta IOJ = \Delta EOJ\) nên
\({S_{EFGHIJ}} = 6{S_{\Delta EOF}} = 6.\frac{{9\sqrt 3 }}{8} = \frac{{27\sqrt 3 }}{4}\left( {c{m^2}} \right)\)