Giải bài tập 9 trang 128 SGK Toán 9 tập 2 - Kết nối tri thức
Để đo khoảng cách giữa hai điểm A và B không tới được, một người đứng ở điểm H sao cho B ở giữa A và H rồi dịch chuyển đến điểm K sao cho KH vuông góc với AB tại H, (HK = aleft( m right)), ngắm nhìn A với (widehat {AKH} = alpha ), ngắm nhìn B với (widehat {BKH} = beta left( {alpha > beta } right)). a) Hãy biểu diễn AB theo (a,alpha ,beta ). b) Khi (a = 3m,alpha = {60^o},beta = {30^o}), hãy tính AB (làm tròn kết quả đến chữ số thập phân thứ ba của mét).
Đề bài
Để đo khoảng cách giữa hai điểm A và B không tới được, một người đứng ở điểm H sao cho B ở giữa A và H rồi dịch chuyển đến điểm K sao cho KH vuông góc với AB tại H, \(HK = a\left( m \right)\), ngắm nhìn A với \(\widehat {AKH} = \alpha \), ngắm nhìn B với \(\widehat {BKH} = \beta \left( {\alpha > \beta } \right)\).
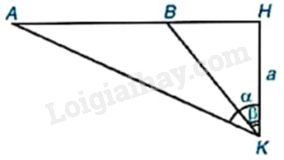
a) Hãy biểu diễn AB theo \(a,\alpha ,\beta \).
b) Khi \(a = 3m,\alpha = {60^o},\beta = {30^o}\), hãy tính AB (làm tròn kết quả đến chữ số thập phân thứ ba của mét).
Phương pháp giải - Xem chi tiết
+ Tam giác KBH vuông tại H nên \(BH = KH.\tan \widehat {HKB} = a.\tan \beta \).
+ Tam giác KAH vuông tại H nên \(AH = KH.\tan \widehat {HKA} = a.\tan \alpha \).
+ Do đó, \(AB = AH - BH = a\left( {\tan \alpha - \tan \beta } \right)\).
Lời giải chi tiết
a) \(\Delta \)KBH vuông tại H nên \(BH = KH.\tan \widehat {HKB} = a.\tan \beta \) (hệ thức giữa cạnh và góc trong tam giác vuông)
\(\Delta \)KAH vuông tại H nên \(AH = KH.\tan \widehat {HKA} = a.\tan \alpha \) (hệ thức giữa cạnh và góc trong tam giác vuông)
Do đó, \(AB = AH - BH = a\left( {\tan \alpha - \tan \beta } \right)\).
b) Với \(a = 3m,\alpha = {60^o},\beta = {30^o}\) ta có: \(AB = 3\left( {\tan {{60}^o} - \tan {{30}^o}} \right) = 3\left( {\sqrt 3 - \frac{{\sqrt 3 }}{3}} \right) = 2\sqrt 3 \approx 3,464\left( m \right)\).