Giải bài tập 9.4 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức
Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại điểm I nằm trong (O) (H.9.9). a) Biết rằng (widehat {AOC} = {60^o},widehat {BOD} = {80^o}). Tính số đo của góc AID. b) Chứng minh rằng (IA.IB = IC.ID).
Đề bài
Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại điểm I nằm trong (O) (H.9.9).
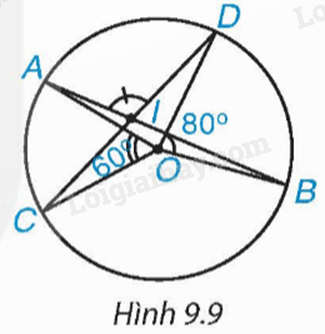
a) Biết rằng \(\widehat {AOC} = {60^o},\widehat {BOD} = {80^o}\). Tính số đo của góc AID.
b) Chứng minh rằng \(IA.IB = IC.ID\).
Phương pháp giải - Xem chi tiết
a) + Sử dụng mối liên hệ giữa góc nội tiếp và cung bị chắn suy ra: $\widehat{IAC}=\frac{1}{2}sđ\overset\frown{CB},\widehat{ACI}=\frac{1}{2}sđ\overset\frown{AD}$.
+ Sử dụng mối liên hệ giữa góc ở tâm và cung bị chắn suy ra: \(sđ\overset\frown{DB}=\widehat{DOB}={{80}^{o}},sđ\overset\frown{AC}=\widehat{AOC}={{60}^{o}}\).
+ Tính được tổng \(\widehat {IAC} + \widehat {ACI}\).
+ Sử dụng tính chất góc ngoài tam giác tính được: \(\widehat {AID} = \widehat {IAC} + \widehat {ACI}\).
b) Sử dụng mối liên hệ giữa góc nội tiếp và cung bị chắn suy ra \(\widehat {IAD} = \widehat {ICB}\).
Chứng minh $\Delta IAD\backsim \Delta ICB\left( g-g \right)\Rightarrow IA.IB=IC.ID$.
Lời giải chi tiết
a) Xét đường tròn tâm (O) có:
+ Vì góc IAC là góc nội tiếp chắn cung BC nên $\widehat{IAC}=\frac{1}{2}sđ\overset\frown{CB}$.
+ Vì góc ACI là góc nội tiếp chắn cung AD nên $\widehat{ACI}=\frac{1}{2}sđ\overset\frown{AD}$.
+ Vì góc DOB là góc ở tâm chắn cung DB nên \(sđ\overset\frown{DB}=\widehat{DOB}={{80}^{o}}\)
+ Vì góc AOC là góc ở tâm chắn cung AC nên \(sđ\overset\frown{AC}=\widehat{AOC}={{60}^{o}}\)
Ta có: $\widehat{IAC}+\widehat{ACI}=\frac{sđ\overset\frown{CB}+sđ\overset\frown{AD}}{2}=\frac{{{360}^{o}}-sđ\overset\frown{DB}-sđ\overset\frown{AC}}{2}=\frac{{{220}^{o}}}{2}={{110}^{o}}$
Vì góc AID là góc ngoài tại đỉnh I của tam giác AIC nên: \(\widehat {AID} = \widehat {IAC} + \widehat {ACI} = {110^o}\)
b) Vì hai góc nội tiếp IAD và ICB cùng chắn cung DB của đường tròn (O) nên \(\widehat {IAD} = \widehat {ICB}\)
Lại có: \(\widehat {AID} = \widehat {CIB}\) (hai góc đối đỉnh)
Do đó, $\Delta IAD\backsim \Delta ICB\left( g-g \right)\Rightarrow \frac{IA}{IC}=\frac{ID}{IB}\Rightarrow IA.IB=IC.ID$ (đpcm)