Giải Câu hỏi trắc nghiệm trang 47,48 sách bài tập Toán 7 Kết nối tri thức với cuộc sống
1. Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia ON là tia đối của tia OM. Khi đó cặp góc đối đỉnh là cặp góc nào trong các cặp góc sau đây?
1.
Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia ON là tia đối của tia OM. Khi đó cặp góc đối đỉnh là cặp góc nào trong các cặp góc sau đây?
|
A. \(\widehat {BOM}\) và \(\widehat {CON}\) |
B.\(\widehat {AOB}\) và \(\widehat {AON}\) |
|
C. \(\widehat {AOM}\) và \(\widehat {CON}\) |
D. \(\widehat {COM}\) và \(\widehat {CON}\). |
Phương pháp giải:
+ Vẽ hình
+ Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Lời giải chi tiết:
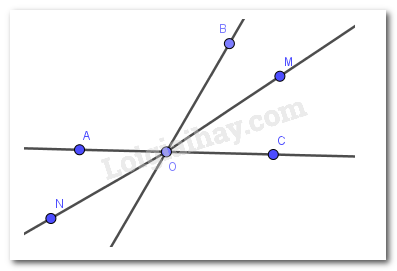
Cặp góc đối đỉnh là cặp góc \(\widehat {AOM}\) và \(\widehat {CON}\)
Chọn C
2.
Trong các khẳng định sau, khẳng định nào đúng?
A. Hai góc bằng nhau thì đối đỉnh;
B. Hai góc không đối đỉnh thì không bằng nhau;
C. Hai góc đối đỉnh thì bằng nhau;
D. Cả ba khẳng định trên đều đúng.
Phương pháp giải:
Tính chất 2 góc đối đỉnh
Lời giải chi tiết:
A. Sai vì 2 góc bằng nhau chưa chắc đã đối đỉnh
B. Sai vì 2 góc không đối đỉnh cũng có thể bằng nhau (chỉ cần số đo của chúng bằng nhau)
C. Đúng
Chọn C
3.
Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Biết số đo của một trong bốn góc đó là \({65^0}\). Khi đó số đo của ba góc còn lại là:
|
A.\({65^0};{110^0};{120^0};\) |
B. \({65^0};{65^0};{115^0};\) |
|
C. \({115^0};{115^0};{50^0};\) |
D. \({65^0};{115^0};{115^0}.\) |
Phương pháp giải:
Hai góc đối đỉnh thì bằng nhau
Hai góc kề bù có tổng số đo là 180 độ.
Lời giải chi tiết:
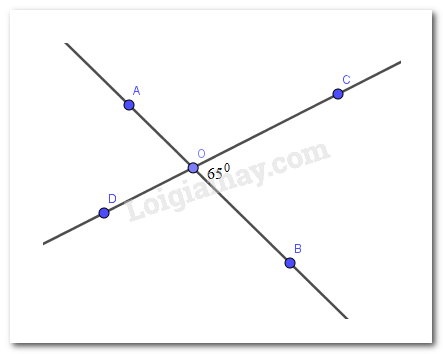
Giả sử hai đường thẳng AB và CD cắt nhau tại O, tạo ra góc BOC có số đo \(65^0\)
\(\Rightarrow \widehat{AOD}=\widehat{BOC}=65^0\) (2 góc đối đỉnh)
\(\widehat{AOB}+\widehat{BOC}=180^0\) (2 góc kề bù) nên \(\widehat{AOB}=180^0-65^0=115^0\)
\(\widehat{COD}=\widehat{AOB}=115^0\) (2 góc đối đỉnh)
Chọn D
4.
Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Số đo của bốn góc đó có thể là trường hợp nào trong các trường hợp sau đây?
|
A.\({70^0};{70^0};{70^0};{110^0}\) |
B. \({60^0};{120^0};{120^0};{120^0};\) |
|
C. \({80^0};{50^0};{130^0};{100^0};\) |
D. \({90^0};{90^0};{90^0};{90^0}.\) |
Phương pháp giải:
Hai góc đối đỉnh thì bằng nhau
Hai góc kề bù có tổng số đo là 180 độ.
Lời giải chi tiết:
2 đường thẳng cắt nhau tạo thành 2 cặp góc đối đỉnh
Mà 2 góc đối đỉnh thì bằng nhau
Chọn D
5.
Hai đường thẳng AB và CD cắt nhau tại O. Cho OM là tia phân giác của góc BOD và \(\widehat {BOM} = {30^0}\). Số đo của góc AOC bằng:
|
A.\({30^0};\) |
B. \({60^0};\) |
|
C. \({120^0};\) |
D. Một kết quả khác. |
Phương pháp giải:
Nếu OM là tia phân giác của góc BOD thì \(\widehat{BOM}=\widehat{MOD}=\dfrac{1}{2}.\widehat{BOD}\)
Hai góc đối đỉnh thì bằng nhau
Lời giải chi tiết:
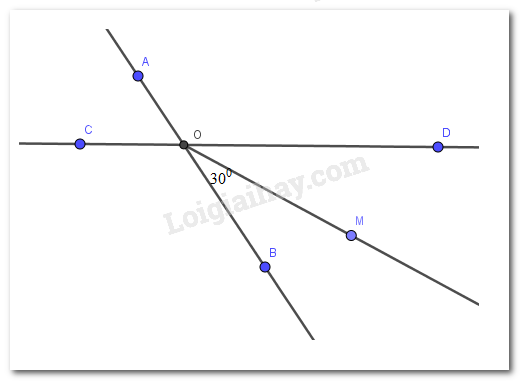
Vì OM là tia phân giác của góc BOD thì \(\widehat{BOM}=\widehat{MOD}=\dfrac{1}{2}.\widehat{BOD}\) nên \(\widehat{BOD}=2. \widehat{BOM}=2.30^0=60^0\)
Ta có: \(\widehat{AOC}=\widehat{BOD}\) ( 2 góc đối đỉnh)
Do đó, \(\widehat{AOC}=60^0\)
Chọn B
6.
Cho hình 3.29.
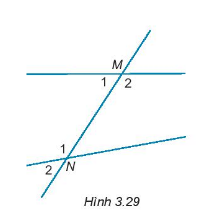
a) Cặp góc so le trong là cặp góc
|
A.\(\widehat {{M_1}},\widehat {{M_2}};\) |
B. \(\widehat {{M_1}},\widehat {{N_1}};\) |
|
C. \(\widehat {{M_1}},\widehat {{N_2}};\) |
D. \(\widehat {{M_2}},\widehat {{N_1}}.\) |
b) Cặp góc đồng vị là cặp góc:
|
A.\(\widehat {{M_1}},\widehat {{M_2}};\) |
B. \(\widehat {{M_1}},\widehat {{N_1}};\) |
|
C. \(\widehat {{M_1}},\widehat {{N_2}};\) |
D. \(\widehat {{M_2}},\widehat {{N_1}}.\) |
Phương pháp giải:
Nhận biết các góc ở vị trí đặc biệt.
Lời giải chi tiết:
a) Chọn D
b) Chọn C
7.
Cho hình 3.30. Cặp góc \(\widehat {{A_1}};\widehat {{B_1}}\) là cặp góc:
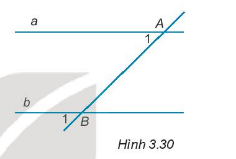
A. So le trong;
B. Đối đỉnh;
C. Đồng vị;
D. Cả ba phương án trên đều sai.
Phương pháp giải:
Nhận biết các góc ở vị trí đặc biệt
Lời giải chi tiết:
\(\widehat {{A_1}};\widehat {{B_1}}\) là cặp góc đồng vị
Chọn C
8.
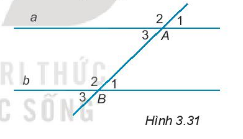
Cho Hình 3.31, đường thẳng a song song với đường thẳng b nếu
A.\(\widehat {{A_1}} = \widehat {{B_2}}\)
B. \(\widehat {{A_2}} = \widehat {{B_3}}\)
C. \(\widehat {{A_3}} = \widehat {{B_2}}\)
D. \(\widehat {{A_3}} = \widehat {{B_1}}\)
Phương pháp giải:
Dấu hiệu nhận biết hai đường thẳng song song.
Lời giải chi tiết:
a//b nếu đường thẳng c cắt hai đường thẳng a và b, tạo thành 1 cặp góc so le trong bằng nhau hoặc 1 cặp góc đồng vị bằng nhau.
Xét khẳng định D:
\(\widehat {{A_3}} = \widehat {{B_1}}\)
Mà 2 góc này ở vị trí so le trong
Do đó, a//b
Chọn D
9.
Cho Hình 3.32, biết \(a// b\).
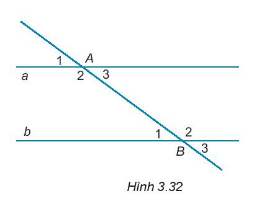
Khẳng định nào sau đây là sai ?
A.\(\widehat {{A_1}} > \widehat {{B_1}}\)
B. \(\widehat {{A_2}} = \widehat {{B_2}}\)
C. \(\widehat {{A_3}} = \widehat {{B_1}}\)
D. \(\widehat {{A_3}} = \widehat {{B_3}}\)
Phương pháp giải:
Tính chất 2 đường thẳng song song
Lời giải chi tiết:
Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_1}};\widehat {{A_2}} = \widehat {{B_2}}; \widehat {{A_3}} = \widehat {{B_3}}\) ( 2 góc đồng vị);
\(\widehat {{A_3}} = \widehat {{B_1}}\) ( 2 góc so le trong)
Vậy khẳng định A sai; B,C,D đúng
Chọn A