Giải câu hỏi trang 53, 54, 55 SGK Toán 8 - Cùng khám phá
Xét tam giác \(ABC\) và tam giác \(A'B'C'\)
Hoạt động
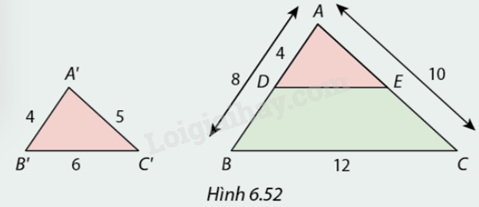
Xét tam giác \(ABC\) và tam giác \(A'B'C'\) có độ dài cạnh như trong hình 6.52.
Đường thẳng \(DE\) song song với cạnh \(BC.\)
1. Vì sao \(\Delta ADE∽\Delta ABC?\)
2. Tính độ dài \(AE\) và \(DE\). Vì sao \(\Delta ADE = \Delta A'B'C'?\)
Em có kết luận gì về \(\Delta \,ABC\)và \(\Delta A'B'C'?\)
Phương pháp giải:
Dựa vào định nghĩa và định lí hai tam giác đồng dạng để chứng minh \(\Delta ADE∽\Delta ABC\).
Sau đó tính độ dài \(AE\) và \(DE\).
Lời giải chi tiết:
1. Xét tam giác \(ADE\) và tam giác \(ABC\), có:
Đường thẳng DE cắt AB tại D, cắt AC tại E
Mà \(DE//BC\).
Áp dụng định lí hai tam giác đồng dạng suy ra \(\Delta ADE\)∽\(\Delta ABC\).
2. Vì \(\Delta ADE\)∽\(\Delta ABC\).
\(\begin{array}{l} = > \frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\\ \Leftrightarrow \frac{4}{8} = \frac{{AE}}{{10}} = \frac{{DE}}{{12}}\\ \Rightarrow AE = 5;DE = 6\end{array}\)
Xét tam giác \(A'B'C'\) và tam giác \(ADC\), ta có:
\(\begin{array}{l}A'B' = AD = 4\\A'C' = AE = 5\\B'C' = DE = 6\end{array}\)
=> \(\Delta ADE = \Delta A'B'C'\)
Luyện tập
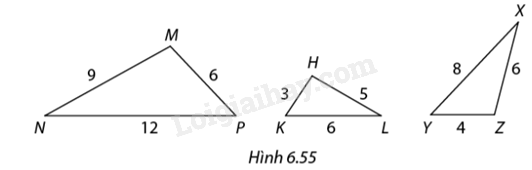
Chỉ ra các cặp tam giác đồng dạng trong Hình 6.55. Viết kí hiệu về sự đồng dạng của chúng và xác định tỉ số đồng dạng.
Phương pháp giải:
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải chi tiết:
Ta có: \(\Delta MNP\)∽\(\Delta XYZ\):
\(\begin{array}{l}\frac{{MP}}{{YZ}} = \frac{6}{4} = \frac{3}{2}\\\frac{{MN}}{{ZX}} = \frac{9}{6} = \frac{3}{2}\\\frac{{NP}}{{XY}} = \frac{{12}}{8} = \frac{3}{2}\end{array}\)
Vận dụng
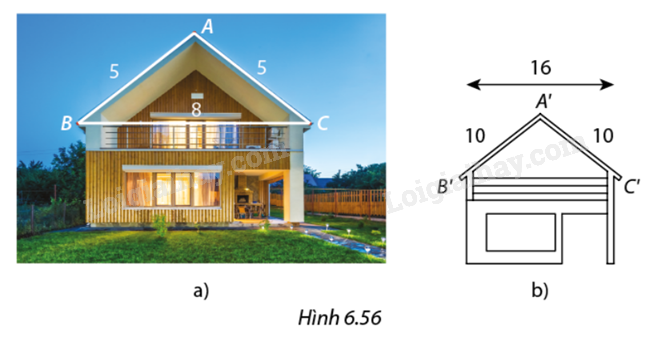
Trên bản vẽ thiết kế mặt tiền ngôi nhà ở Hình 5.65b, khoảng cách thực tế giữa các đỉnh \(A',B',C'\) của mái nhà là \(A'B' = A'C' = 10\,cm,B'C' = 16\,cm.\) Trên thực tế, mái nhà được xây dựng có kích thước \(AB = AC = 5\,m\) và \(BC = 8\,m\) (Hình 5.56a). Hỏi mặt tiền của mái nhà có được xây dựng đúng với hình dạng như được thiết kế không?
Phương pháp giải:
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải chi tiết:
Để mặt tiền của mái nhà được xây đúng với hình dạng như được thiết kế thì:
\(\Delta ABC\)∽\(\Delta A'B'C'\)
\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}}\)
Mà
\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{5}{{10}} = \frac{1}{2}\\\frac{{AC}}{{A'C'}} = \frac{5}{{10}} = \frac{1}{2}\\\frac{{BC}}{{B'C'}} = \frac{8}{{16}} = \frac{1}{2}\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{2}\end{array}\)
Vậy mặt tiền của mái nhà được xây đúng với hình dạng như được thiết kế.