Giải tuần 26: Luyện tập chung (trang 27)
Tính. Tìm x. Viết tiếp vào chỗ chấm cho thích hợp: Một con kênh dài 15km. Người ta đã kè được hai bên bờ của con kênh với độ dài bằng 2/5 độ dài của toàn con kênh.
Bài 1
Tính:
a) \(\dfrac{4}{3}:\dfrac{2}{5} = \ldots \) \(\dfrac{1}{8}:7 = \ldots \)
b) \(3:\dfrac{4}{5} = \ldots \) \(\dfrac{4}{5}:3 = \ldots \)
Phương pháp giải:
- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
- Viết số tự nhiên dưới dạng phân số có mẫu số là \(1\), sau đó thực hiện phép chia hai phân số như thông thường
Lời giải chi tiết:
a) \(\dfrac{4}{3}:\dfrac{2}{5} = \dfrac{4}{3} \times \dfrac{5}{2} = \dfrac{{4 \times 5}}{{3 \times 2}}\)\( = \dfrac{{2 \times 2 \times 5}}{{3\times 2}} = \dfrac{{10}}{3}\)
\(\dfrac{1}{8}:7 = \dfrac{1}{8}:\dfrac{7}{1} = \dfrac{1}{8} \times \dfrac{1}{7} = \dfrac{1}{{56}}\)
b) \(3:\dfrac{4}{5} = \dfrac{3}{1}:\dfrac{4}{5} = \dfrac{3}{1} \times \dfrac{5}{4} = \dfrac{{15}}{4}\)
\(\dfrac{4}{5}:3 = \dfrac{4}{5}:\dfrac{3}{1} = \dfrac{4}{5} \times \dfrac{1}{3} = \dfrac{4}{{15}}\)
Bài 2
Tìm \(x\) :
\(\dfrac{3}{{10}} \times x = \dfrac{2}{5}\) \(\dfrac{1}{8}:x = \dfrac{1}{2}\)
Phương pháp giải:
Xác định vị trí của \(x\) rồi tìm \(x\) theo một số quy tắc:
- Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
- Muốn tìm số chia ta lấy số bị chia chia cho thương.
Lời giải chi tiết:
\(\begin{array}{l}\dfrac{3}{{10}} \times x = \dfrac{2}{5}\\\,\,\,\,\,\,\,\,\,\;\;\;\;x = \dfrac{2}{{5}}:\dfrac{3}{10}\\\,\,\,\,\,\,\,\,\,\;\;\;\;x = \dfrac{4}{3}\end{array}\)
\(\begin{array}{l}\dfrac{1}{8}:x = \dfrac{1}{2}\\\,\,\,\,\,\,\,\;\;x = \dfrac{1}{8}:\dfrac{1}{2}\\\,\,\,\,\,\,\,\;\;x = \dfrac{1}{4}\end{array}\)
Bài 3
Viết tiếp vào chỗ chấm cho thích hợp:
Một con kênh dài \(15km\). Người ta đã kè được hai bên bờ của con kênh với độ dài bằng \(\dfrac{2}{5}\) độ dài của toàn con kênh.
a) Độ dài phần đã được kè của con kênh là ..............
b) Độ dài phần chưa được kè của con kênh là ..........
Phương pháp giải:
- Tìm độ dài phần được kè của con kênh ta lấy độ dài của toàn con kênh nhân với \(\dfrac{2}{5}\).
- Tìm độ dài phần chưa được kè của con kênh ta lấy độ dài toàn con kênh trừ đi độ dài phần đã được kè của con kênh.
Lời giải chi tiết:
a) Độ dài phần đã được kè của con kênh là:
\(15 \times \dfrac{2}{5} = 6\,\,(km)\)
b) Độ dài phần chưa được kè của con kênh là:
\(15 - 6 = 9\,\,(km)\)
Đáp số: a) \(6km\);
b) \(9km.\)
Bài 4
Viết tiếp vào chỗ chấm để được đáp số đúng:
Mẹ cho Minh \(100\; 000\) đồng để mua đồ dùng học tập. Minh mua bút hết \(\dfrac{1}{4}\) số tiền và mua vở hết \(\dfrac{3}{5}\) số tiền. Hỏi Minh còn lại bao nhiêu tiền?
Phương pháp giải:
- Tìm số tiền Minh mua bút ta lấy số tiền ban đầu mẹ cho nhân với \(\dfrac{1}{4}\).
- Tìm số tiền Minh mua vở ta lấy số tiền ban đầu mẹ cho nhân với \(\dfrac{3}{5}\).
- Tìm số tiền còn lại ta lấy số tiền ban đầu mẹ cho Minh trừ đi tổng số tiền Minh mua bút và vở.
Lời giải chi tiết:
Minh mua bút hết số tiền là:
\(100\,000 \times \dfrac{1}{4} = 25\,000\) (đồng)
Minh mua vở hết số tiền là:
\(100\,000 \times \dfrac{3}{5} = 60\,000\) (đồng)
Minh còn lại số tiền là:
\(100\,000 - (25\,000 + 60\,000) = 15\,000\) (đồng)
Đáp số: \(15\,000\) đồng.
Bài 5
Tính:
a) \(\dfrac{5}{3} + \dfrac{2}{5} = \ldots \) \(\dfrac{5}{7} + \dfrac{9}{{14}} = \ldots \)
b) \(\dfrac{7}{3} - \dfrac{1}{4} = \ldots \) \(\dfrac{9}{{10}} - \dfrac{3}{4} = \ldots \)
Phương pháp giải:
- Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:
a) \(\dfrac{5}{3} + \dfrac{2}{5} = \dfrac{{25}}{{15}} + \dfrac{{6}}{{15}} = \dfrac{{31}}{{15}}\)
\(\dfrac{5}{7} + \dfrac{9}{{14}} = \dfrac{{10}}{{14}} + \dfrac{9}{{14}} = \dfrac{{19}}{{14}}\)
b) \(\dfrac{7}{3} - \dfrac{1}{4} = \dfrac{{28}}{{12}} - \dfrac{3}{{12}} = \dfrac{25}{{12}}\)
\(\dfrac{9}{{10}} - \dfrac{3}{4} = \dfrac{{18}}{{20}} - \dfrac{{15}}{{20}} = \dfrac{3}{{20}}\)
Bài 6
Tính:
a) \(\dfrac{3}{2} \times \dfrac{4}{5} + \dfrac{2}{3} = \ldots \)
b) \(\dfrac{7}{4} - \dfrac{3}{4}:\dfrac{5}{6} = \ldots \)
Phương pháp giải:
Biểu thức có chứa phép cộng, phép trừ, phép nhân, phép chia thì ta thực hiện phép nhân, phép chia trước; thực hiện phép cộng, phép trừ sau.
Lời giải chi tiết:
a) \(\dfrac{3}{2} \times \dfrac{4}{5} + \dfrac{2}{3} = \dfrac{{12}}{10} + \dfrac{2}{3}\)\( = \dfrac{{6}}{5} + \dfrac{2}{3} = \dfrac{{18}}{15} + \dfrac{10}{15}= \dfrac{{28}}{15}\)
b) \(\dfrac{7}{4} - \dfrac{3}{4}:\dfrac{5}{6} = \dfrac{7}{4} - \dfrac{3}{4} \times \dfrac{6}{5} \)\(= \dfrac{7}{4} - \dfrac{9}{10} = \dfrac{{35}}{{20}} - \dfrac{{18}}{{20}} = \dfrac{{17}}{{20}}\)
Bài 7
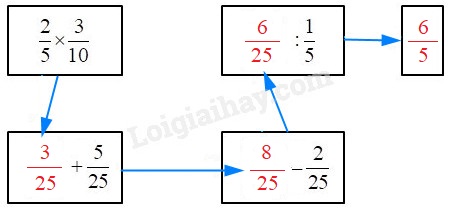
Viết kết quả của phép tính vào ô trống :

Phương pháp giải:
Áp dụng các quy tắc cộng, trừ, nhân, chia hai phân số rồi tính lần lượt theo hướng mũi tên.
Lời giải chi tiết:
\(\begin{array}{l}\dfrac{2}{5} \times \dfrac{3}{{10}} = \dfrac{{2 \times 3}}{{5 \times 10}} = \dfrac{{2 \times 3}}{{5 \times 5 \times 2}} = \dfrac{3}{{25}}\\\dfrac{3}{{25}} + \dfrac{5}{{25}} = \dfrac{8}{{25}}\\\dfrac{8}{{25}} - \dfrac{2}{{26}} = \dfrac{6}{{25}}\end{array}\)
\(\dfrac{6}{{25}}:\dfrac{1}{5} = \dfrac{6}{{25}} \times \dfrac{5}{1} = \dfrac{{6 \times 5}}{{25 \times 1}}\)\(= \dfrac{{6 \times 5}}{{5 \times 5 \times 1}} = \dfrac{6}{5}\)
Vậy ta có kết quả như sau:
Bài 8
Hằng ngày, Huy thường dậy sớm và tập thể dục bằng cách chạy bộ. Để biết mỗi ngày mình chạy bộ được bao xa, Huy đã ghi khoảng cách từ nhà đến một số địa điểm như bảng dưới đây:
|
Địa điểm |
Khoảng cách |
|
Công viên |
\(\dfrac{5}{4}km\) |
|
Nhà hàng |
\(\dfrac{3}{5}km\) |
|
Chợ |
\(\dfrac{1}{3}km\) |
Viết tiếp vào chỗ chấm cho thích hợp:
a) Nếu Huy chạy bộ từ nhà đến công viên rồi quay trở về nhà thì Huy chạy được ....... km.
b) Nếu Huy chạy bộ hai vòng từ nhà đến chợ thì Huy chạy được ....... km.
c) Nếu Huy chạy bộ ba vòng từ nhà đến nhà hàng thì Huy chạy được ....... km.
Lưu ý: Một vòng từ địa điểm A đến địa điểm B được tính là từ A đến B rồi quay trở về A.
Phương pháp giải:
- Nếu Huy chạy bộ từ nhà đến công viên rồi quay trở về nhà thì Huy chạy được quãng đường dài gấp 2 lần quãng đường từ nhà đến công viên.
- Một vòng từ nhà đến chợ sẽ bằng 2 lần độ dài từ nhà đến chợ. Muốn tính quãng đường Huy chạy bộ 2 vòng từ nhà đến chợ ta lấy độ dài một vòng từ nhà đến chợ nhân với 2.
- Một vòng từ nhà đến nhà hàng sẽ bằng 2 lần độ dài từ nhà đến nhà hàng. Muốn tính quãng đường Huy chạy bộ 3 vòng từ nhà đến nhà hàng ta lấy độ dài một vòng từ nhà đến nhà hàng nhân với 3.
Lời giải chi tiết:
a) Nếu Huy chạy bộ từ nhà đến công viên rồi quay trở về nhà thì Huy chạy được số ki-lô-mét là:
\(\dfrac{5}{4} \times 2 = \dfrac{5}{2}\,\,(km)\)
b) Huy chạy bộ một vòng từ nhà đến chợ được số ki-lô-mét là:
\(\dfrac{1}{3} \times 2 = \dfrac{2}{3}\,\,(km)\)
Nếu Huy chạy bộ hai vòng từ nhà đến chợ thì Huy chạy được số ki-lô-mét là:
\(\dfrac{2}{3} \times 2 = \dfrac{4}{3}\,\,(km)\)
c) Huy chạy bộ một vòng từ nhà đến nhà hàng được số ki-lô-mét là:
\(\dfrac{3}{5} \times 2 = \dfrac{6}{5}\,\,(km)\)
Nếu Huy chạy bộ ba vòng từ nhà đến nhà hàng thì Huy chạy được số ki-lô-mét là:
\(\dfrac{6}{5} \times 3 = \dfrac{18}{5}\,\,(km)\)
Đáp số : a) \(\dfrac{5}{2}km\;;\)
b) \(\dfrac{4}{3}km\;;\)
c) \(\dfrac{18}{5}km.\)
Vui học
Viết tiếp vào chỗ chấm để được câu trả lời đúng:
Một cửa hàng xăng, buổi sáng bán được \(1275l\), buổi chiều bán được số xăng bằng \(\dfrac{1}{3}\) buổi sáng thì cửa hàng còn lại \(5620l\). Hỏi lúc đầu cửa hàng có bao nhiêu lít xăng?
Phương pháp giải:
- Tính số lít xăng buổi chiều cửa hàng bán được ta lấy số lít xăng buổi sáng cửa hàng bán được nhân với \(\dfrac{1}{3}\).
- Tính số lít xăng ban đầu cửa hàng có ta lấy số lít xăng còn lại sau khi bán cộng với tổng số lít xăng buổi sáng và buổi chiều cửa hàng bán được.
Lời giải chi tiết:
Buổi chiều cửa hàng bán được số lít xăng là:
\(1275 \times \dfrac{1}{3} = 425\;(l)\)
Lúc đầu cửa hàng có số lít xăng là:
\( 5620+1275 + 425 = 7320\;(l)\)
Đáp số : \(7320l.\)