Giải mục 1 trang 14, 15 SGK Toán 11 tập 2 - Cùng khám phá
Cho biểu thức \(y = {2^x}\), trong đó x là một số thực lấy giá trị tùy ý.
Hoạt động 1
Cho biểu thức \(y = {2^x}\), trong đó x là một số thực lấy giá trị tùy ý.
a) Hãy tính giá trị của y tương ứng với mỗi giá trị của x được cho trong bảng sau:

b) Với mỗi giá trị của x, ta tính được bao nhiêu giá trị của y? y có phải là hàm số của x không? Vì sao?
c) Biểu thức \(y = {\left( { - 3} \right)^x}\) có xác định một hàm số khi x lấy giá trị trong tập số thực \(\mathbb{R}\) không? Vì sao?
Phương pháp giải:
a) Thay x = 3; 0,5; \( - \frac{3}{7}\); \(\sqrt 2 \); \( - \sqrt 3 \) vào biểu thức \(y = {2^x}\).
b) Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.
c) Khi số mũ nằm trong khoảng (0;1) thì cơ số không thể âm.
Lời giải chi tiết:
a)

b) Với mỗi giá trị của x chỉ tính được một giá trị của y. y là hàm số của x vì mỗi một giá trị của x thì ta luôn xác định được chỉ một giá trị tương ứng của y.
c) Biểu thức \(y = {\left( { - 3} \right)^x}\) không xác định một hàm số khi x lấy giá trị trong tập số thực \(\mathbb{R}\). Vì khi \(x = \frac{1}{2}\), ta có: \({\left( { - 3} \right)^{\frac{1}{2}}} = \sqrt { - 3} \) (Vô lí)
Luyện tập 1
Trong các hàm số sau, hàm số nào là hàm số mũ, với cơ số bao nhiêu? Vì sao?
a) \(y = {3^{2x}}\)
b) \(y = {\left( { - \pi } \right)^x}\)
c) \(y = {x^{ - 4}}\)
d) \(y = {4^{ - x}}\)
Phương pháp giải:
Hàm số \(y = {a^x}\) được gọi là hàm số mũ cơ số a với a là một số thực dương khác 1.
Lời giải chi tiết:
a) \(y = {3^{2x}}\) là hàm số mũ với cơ số bằng 3.
b) \(y = {\left( { - \pi } \right)^x}\) là hàm số mũ với cơ số bằng \(\pi \).
c) \(y = {x^{ - 4}}\) không là hàm số mũ vì cơ số không phải hằng số.
d) \(y = {4^{ - x}}\) là hàm số mũ với cơ số bằng 4.
Hoạt động 2
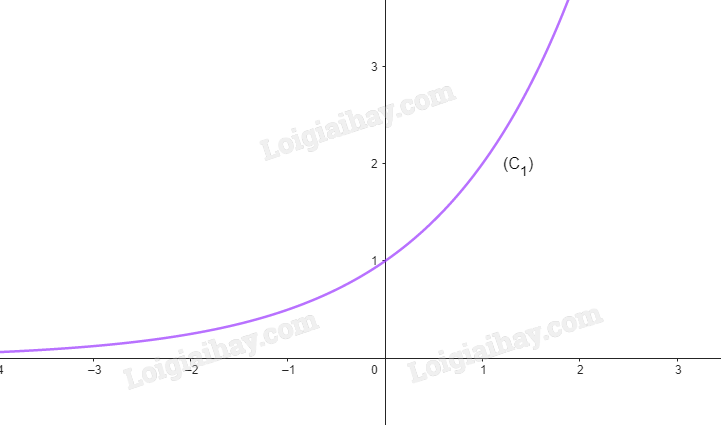
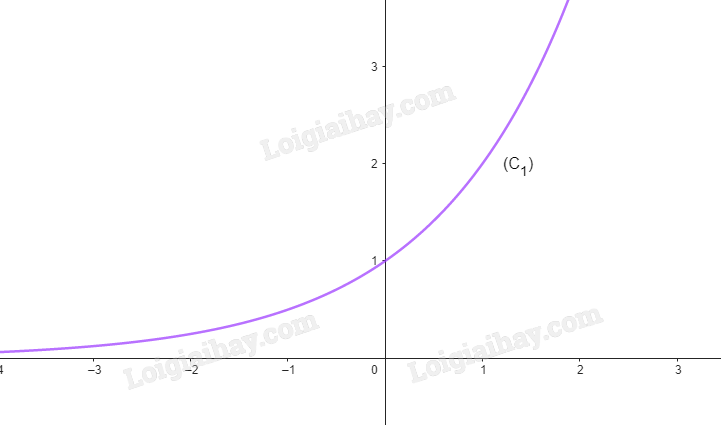
Cho hàm số \(y = {2^x}\) có đồ thị là (C 1 ) và hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) có đồ thị (C 2 ).
a) Hoàn thành bảng giá trị sau và biểu diễn trong mặt phẳng Oxy:

b) Vẽ đường cong nối các điểm thuộc (C 1 ) (Theo thứ tự hoành độ tăng dần) và một đường cong khác nối các điểm thuộc (C 2 ) (Theo thứ tự hoành độ tăng dần).
Phương pháp giải:
Thay x = -3, -2,… , 3 vào \(y = {2^x}\) và \(y = {\left( {\frac{1}{2}} \right)^x}\)
Lời giải chi tiết:
a,
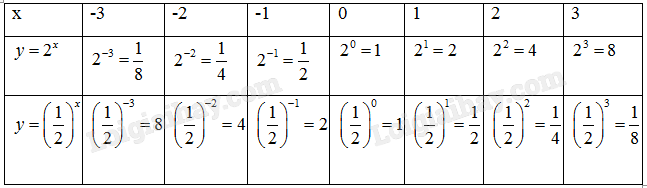
b)
Luyện tập 2
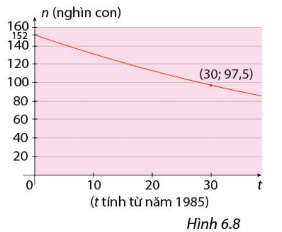
Đồ thị Hình 6.8 cho thấy số lượng hươu cao cổ trên thế giới suy giảm nghiêm trọng trong 30 năm qua (từ năm 1985 đến 2015) (nguồn: https://tuoitre.vn/huou-cao-co-sap-vao-danh -sach-loai-gap-nguy-hiem-20190428162017473.htm). Giả sử rằng số lượng hươu ở đây giảm theo hàm số \(n\left( t \right) = C.{a^t}\).
a) Tìm số lượng hươu vào năm 1985.
b) Tìm hàm số biểu diễn số lượng hươu sau t năm kể từ năm 1985.
c) Dự đoán số lượng hươu vào năm 2025.
Phương pháp giải:
a) Năm 1985 là t = 0, quan sát đồ thị khi t = 0 thì n bằng bao nhiêu.
b) Số lượng hươu mỗi năm là số lượng hươu năm 1985 trừ đi số lượng hươu giảm được tính theo hàm số \(n\left( t \right) = C.{a^t}\).
c) Kể từ năm 1985 đến 2025 là 40 năm nên t = 40. Thay t = 40 vào hàm số ở phần b.
Lời giải chi tiết:
a) Số lượng hươu năm 1985 là 152 nghìn con.
b) Ta có: \(C.{a^0} = n\left( 0 \right) \Leftrightarrow C = 152\)
\(\begin{array}{l}C.{a^{30}} = n\left( {30} \right)\\ \Leftrightarrow 152.{a^{30}} = 97,5\\ \Leftrightarrow {a^{30}} = \frac{{195}}{{304}}\\ \Leftrightarrow a = \sqrt[{30}]{{\frac{{195}}{{304}}}}\end{array}\)
\( \Rightarrow n\left( t \right) = 152.{\left( {\sqrt[{30}]{{\frac{{195}}{{304}}}}} \right)^t}\)
Hàm số biểu diễn lượng hươu sau t năm kể từ năm 1985 là: \(H\left( t \right) = 152 - 152.{\left( {\sqrt[{30}]{{\frac{{195}}{{304}}}}} \right)^t}\)
c) Kể từ năm 1985 đến 2025 là 40 năm nên t = 40
Số lượng hươu vào năm 2025 là: \(H\left( {40} \right) = 152 - 152.{\left( {\sqrt[{30}]{{\frac{{195}}{{304}}}}} \right)^{40}} \approx 67,914\) (nghìn con)