Giải mục 1 trang 8, 9, 10, 11 SGK Toán 11 tập 1 - Cùng khám phá
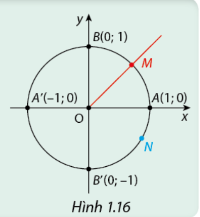
Trên đường tròn lượng giác, gọi M và N lần lượt là điểm biểu diễn của góc lượng giác có số đo \(\frac{{9\pi }}{4}\) và \( - \frac{\pi }{6}\). Tìm tọa độ của M và N.
Hoạt động 1
Trên đường tròn lượng giác, gọi M và N lần lượt là điểm biểu diễn của góc lượng giác có số đo \(\frac{{9\pi }}{4}\) và \( - \frac{\pi }{6}\). Tìm tọa độ của M và N.
Phương pháp giải:
Áp dụng công thức lượng giác:
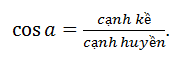
Lời giải chi tiết:
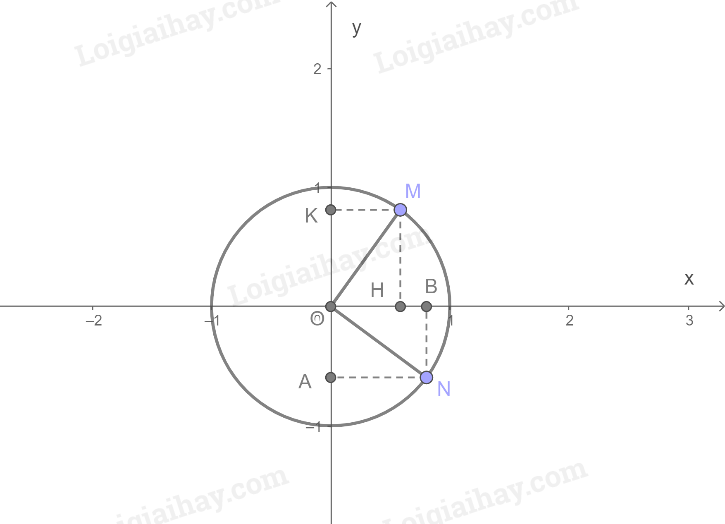
Gọi các điểm như trên hình vẽ
Gọi x và y lần lượt là hoành độ và tung độ của M \(\left( {x > 0,y > 0} \right)\)
Vì tam giác OMH vuông tại H và có góc \(\widehat {MOH} = \frac{\pi }{4}\) nên \(OH = OM.\cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\)
Vì tam giác OKM vuông tại K và có góc \(\widehat {MOK} = \frac{\pi }{4}\) nên \(OK = OM.\cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\).
Mà \(x > 0,y > 0\) nên \(M\left( {\frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right)\)
Gọi z và t là hoành độ và tung độ của N \(\left( {z > 0,t < 0} \right)\)
Vì tam giác OBN vuông tại B có góc \(\widehat {BON} = \frac{\pi }{6}\) nên \(OB = ON.\cos \frac{\pi }{6} = \frac{{\sqrt 3 }}{2}\)
Vì tam giác OAN vuông tại A có góc \(\widehat {AON} = \frac{\pi }{3}\) nên \(OA = ON.\cos \frac{\pi }{3} = \frac{1}{2}\)
Mà \(z > 0,t < 0\) nên \(N\left( {\frac{{\sqrt 3 }}{2}; - \frac{1}{2}} \right)\).
Luyện tập 1
Tìm các giá trị lượng giác của góc 330 0 .
Phương pháp giải:
Áp dụng công thức lượng giác:
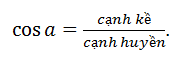
Lời giải chi tiết:
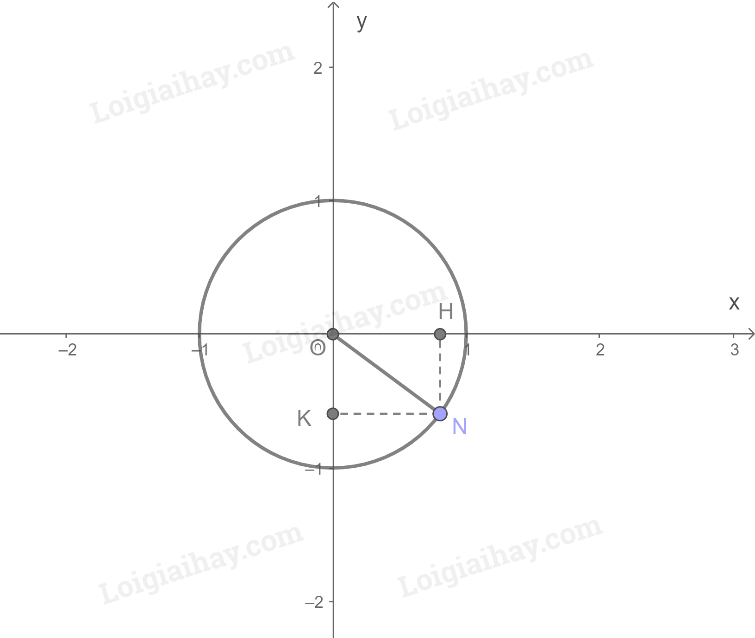
Trên đường tròn lượng giác, gọi M là điểm biểu diễn của góc lượng giác 330 0
Gọi x và y lần lượt là hoành độ và tung độ của M. Ta có: \(x > 0,y < 0\)
Vì tam giác OMH vuông tại H và có góc \(\widehat {MOH} = {30^0}\) nên \(OH = OM.\cos {30^0} = \frac{{\sqrt 3 }}{2}\)
Vì tam giác OKM vuông tại K và có góc \(\widehat {MOK} = {60^0}\) nên \(OK = OM.\cos {60^0} = \frac{1}{2}\)
Suy ra: \(\cos {330^0} = x = \frac{{\sqrt 3 }}{2}\), \(\sin {330^0} = y = - \frac{1}{2}\)
\( \Rightarrow \tan {330^0} = \frac{{\sin {{330}^0}}}{{\cos {{330}^0}}} = \left( { - \frac{1}{2}} \right):\frac{{\sqrt 3 }}{2} = - \frac{{\sqrt 3 }}{3}\)
\( \Rightarrow \cot {330^0} = \frac{{\cos {{330}^0}}}{{\sin {{330}^0}}} = \frac{{\sqrt 3 }}{2}:\left( { - \frac{1}{2}} \right) = - \sqrt 3 \)
Hoạt động 2
Hãy viết lại bảng các giá trị lượng giác của một số góc đặc biệt từ 0 0 đến 90 0 đã học ở lớp 10.
Phương pháp giải:
Xem lại sách lớp 10
Lời giải chi tiết:
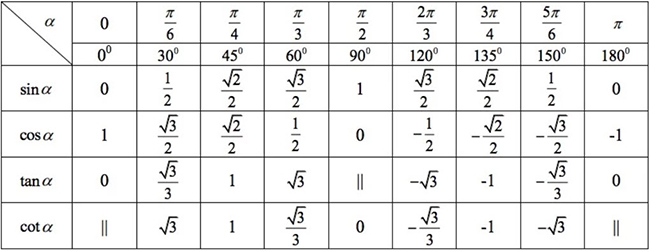
Luyện tập 2
Tính \(\sin \left( { - \frac{{35\pi }}{6}} \right),\cos \left( { - \frac{{35\pi }}{6}} \right),\tan \left( { - \frac{{35\pi }}{6}} \right),\cot \left( { - \frac{{35\pi }}{6}} \right)\).
Phương pháp giải:
\(\begin{array}{l}\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \\\cos \left( {\alpha + k2\pi } \right) = \cos \alpha \\\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\\\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}\sin \left( { - \frac{{35\pi }}{6}} \right) = \sin \left( { - 6\pi + \frac{\pi }{6}} \right) = \sin \left( {\frac{\pi }{6}} \right) = \frac{1}{2}\\\cos \left( { - \frac{{35\pi }}{6}} \right) = \cos \left( { - 6\pi + \frac{\pi }{6}} \right) = \cos \left( {\frac{\pi }{6}} \right) = \frac{{\sqrt 3 }}{2}\\\tan \left( { - \frac{{35\pi }}{6}} \right) = \frac{{\sin \left( { - \frac{{35\pi }}{6}} \right)}}{{\cos \left( { - \frac{{35\pi }}{6}} \right)}} = \frac{{\sqrt 3 }}{3}\\\cot \left( { - \frac{{35\pi }}{6}} \right) = \frac{{\cos \left( { - \frac{{35\pi }}{6}} \right)}}{{\sin \left( { - \frac{{35\pi }}{6}} \right)}} = \sqrt 3 \end{array}\)
Luyện tập 3
Tính \(\sin {315^0},\cos \frac{{12\pi }}{7},\tan \left( { - {{168}^0}} \right)\).
Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
\(\sin \left( {{{315}^0}} \right) = - \frac{{\sqrt 2 }}{2}\)
\(\cos \frac{{12\pi }}{7} \approx 0,62\)
\(\tan \left( { - {{168}^0}} \right) \approx 0,21\)
Vận dụng
Một cánh tay robot dài 1m được điều khiển để gắp một vật tại điểm C, rồi xoay theo chiều dương một góc 225 0 để thả vật tại điểm D như Hình 1.20. Chọn hệ trục tọa độ Oxy sao cho tâm của cánh tay robot trùng với O và C có tọa độ là (1; 0). Tìm tọa độ của vật tại điểm D.
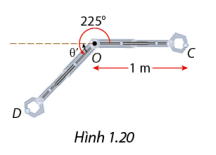
Phương pháp giải:
Hoành độ của điểm D là \(\cos {225^0}\), tung độ của điểm D là \(\sin {225^0}\).
Lời giải chi tiết:
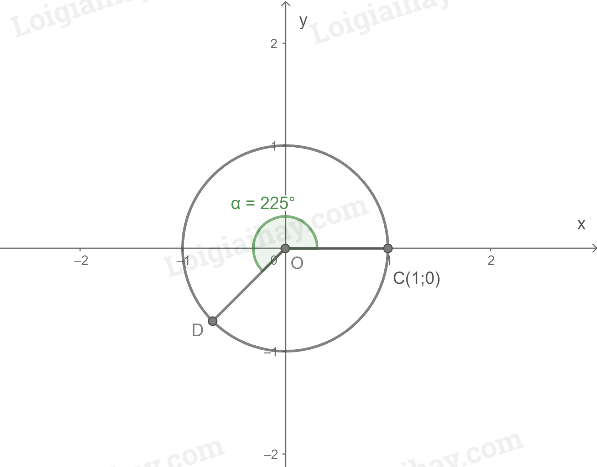
Gọi x và y là hoành độ và tung độ của D
\(\begin{array}{l}x = \cos {225^0} = - \frac{{\sqrt 2 }}{2}\\y = \sin {225^0} = - \frac{{\sqrt 2 }}{2}\end{array}\)
Vậy \(D\left( { - \frac{{\sqrt 2 }}{2}; - \frac{{\sqrt 2 }}{2}} \right)\).