Giải mục 1 trang 20, 21, 22, 23, 24, 25, 26, 27, 28 SGK Toán 11 tập 1 - Cùng khám phá — Không quảng cáo

Hoạt động 1

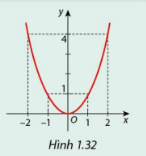
Hàm số $f\left( x \right) = {x^2}$ có đồ thị như Hình 1.32.

a) So sánh $f\left( { - 1} \right)$ và $f\left( 1 \right)$ , $f\left( { - 2} \right)$và $f\left( 2 \right)$, $f\left( { - x} \right)$ và $f\left( x \right)$.

b) Đồ thị của hàm số nhận trục nào làm trục đối xứng?

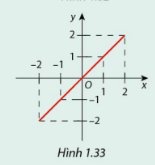
Hàm số $y = f\left( x \right) = x$, với $x \in \left[ { - 2;2} \right]$, có đồ thị như Hình 1.33.

a) So sánh $f\left( { - 1} \right)$ và $f\left( 1 \right)$ , $f\left( { - 2} \right)$và $f\left( 2 \right)$, $f\left( { - x} \right)$ và $f\left( x \right)$ khi $x \in \left[ { - 2;2} \right]$.

b) Đồ thị của hàm số nhận điểm nào làm tâm đối xứng?

Phương pháp giải:

Thay lần lượt $x =  - 1,1, - 2,2, - x,x$ vào hàm số.

Lời giải chi tiết:

Hình 1.32

a)

$\begin{array}{l}f\left( { - 1} \right) = 1 = f\left( 1 \right)\\f\left( { - 2} \right) = 4 = f\left( 2 \right)\\f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2} = f\left( x \right)\end{array}$

b) Đồ thị của hàm số nhận trục Oy làm trục đối xứng.

Hình 1.33

a)

$\begin{array}{l}f\left( { - 1} \right) =  - 1 =  - f\left( 1 \right)\\f\left( { - 2} \right) =  - 2 =  - f\left( 2 \right)\\f\left( { - x} \right) =  - x =  - f\left( x \right)\end{array}$

b) Đồ thị của hàm số nhận điểm $O\left( {0;0} \right)$ làm tâm đối xứng.

Luyện tập 1

Xác định hàm số chẵn, hàm số lẻ trong các hàm số sau:

a) $y = f\left( x \right) = 4x - 3;$

b) $y = g\left( x \right) = 2{x^2} - 6;$

c) $y = h\left( x \right) = {x^3} - 3x.$

Phương pháp giải:

Thay $- x$ vào hàm số.

$f\left( { - x} \right) = f\left( x \right)$ là hàm số chẵn, $f\left( { - x} \right) =  - f\left( x \right)$ là hàm số lẻ.

Lời giải chi tiết:

a)

$\begin{array}{l}D = \mathbb{R}\\\forall x \in D \Rightarrow  - x \in D\end{array}$

$f\left( { - x} \right) = 4\left( { - x} \right) - 3 =  - 4x - 3 \ne f\left( x \right) = 4x - 3$

Vậy hàm số đã cho không phải hàm số chẵn cũng không phải hàm số lẻ.

b)

$\begin{array}{l}D = \mathbb{R}\\\forall x \in D \Rightarrow  - x \in D\end{array}$

$g\left( { - x} \right) = 2{\left( { - x} \right)^2} - 6 = 2{x^2} - 6 = g\left( x \right)$

Vậy hàm số đã cho là hàm số chẵn.

c)

$\begin{array}{l}D = \mathbb{R}\\\forall x \in D \Rightarrow  - x \in D\end{array}$

$h\left( { - x} \right) = {\left( { - x} \right)^3} - 3\left( { - x} \right) =  - {x^3} + 3x =  - \left( {{x^3} - 3x} \right) =  - h\left( x \right)$

Vậy hàm số đã cho là hàm số lẻ.

Hoạt động 2

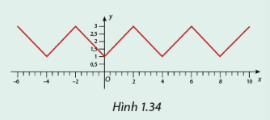
Cho hàm số $y = f\left( x \right)$ có đồ thị như Hình 1.34.

a) So sánh $f\left( { - 4} \right),f\left( 0 \right),f\left( 4 \right),f\left( 8 \right).$.

b) Tìm một số $T \ne 0$ sao cho $f\left( {x + T} \right) = f\left( x \right)$, với x = -6, x = -2, x = 2, x = 6.

c) Nhận xét đồ thị của hàm số trên các đoạn $\left[ { - 4;0} \right],\left[ {0;4} \right]$ và $\left[ {4;8} \right]$.

Phương pháp giải:

a) Tìm tung độ khi hoành độ bằng -4, 0, 4, 8 và so sánh các hoành độ này.

b) Tìm tung độ khi hoành độ bằng -6, -2, 2, 6 và so sánh các hoành độ này. Nhận xét khoảng cách giữa các số -6, -2, 2, 6.

c) Quan sát hình dạng đồ thị trên các đoạn $\left[ { - 4;0} \right],\left[ {0;4} \right]$ và $\left[ {4;8} \right]$.

Lời giải chi tiết:

a) $f\left( { - 4} \right) = f\left( 0 \right) = f\left( 4 \right) = f\left( 8 \right) = 1$

b) $f\left( { - 6} \right) = f\left( { - 2} \right) = f\left( 2 \right) = f\left( 6 \right) = 3$

Vậy T là bội của 4.

c) Đồ thị hàm số  trên các đoạn $\left[ { - 4;0} \right],\left[ {0;4} \right]$ và $\left[ {4;8} \right]$ giống nhau.

Luyện tập 2

Hàm số hằng $y = f\left( x \right) = c$ (c là hằng số) có phải là một hàm số tuần hoàn không? Vì sao?

Phương pháp giải:

Hàm hằng là hàm số mà y không thay đổi $\forall x$.

Lời giải chi tiết:

Hàm hằng là hàm số mà y không thay đổi $\forall x$ nên hàm hằng là hàm số tuần hoàn.