Giải mục 1 trang 16, 17 SGK Toán 11 tập 2 - Kết nối tri thức
a) Tính (y = {2^x}) khi x lần lượt nhận các giá trị - 1; 0; 1. Với mỗi giá trị của x có bao nhiêu giá trị của (y = {2^x}) tương ứng?
HĐ 1
a) Tính \(y = {2^x}\) khi x lần lượt nhận các giá trị - 1; 0; 1. Với mỗi giá trị của x có bao nhiêu giá trị của \(y = {2^x}\) tương ứng?
b) Với những giá trị nào của x, biểu thức \(y = {2^x}\) có nghĩa?
Phương pháp giải:
Thay các giá trị x lần lượt để tính y.
Lời giải chi tiết:
a) Với \(x = - 1\) thì \(y = {2^{ - 1}} = \frac{1}{2}\)
Với \(x = 0\) thì \(y = {2^0} = 1\)
Với \(x = 1\) thì \(y = {2^1} = 2\)
b) Biểu thức \(y = {2^x}\) có nghĩa với mọi giá trị của x.
CH
Trong các hàm số sau, những hàm số nào là hàm số mũ? Khi đó hãy chỉ ra cơ cố.
a) \(y = {\left( {\sqrt 2 } \right)^x};\)
b) \(y = {2^{ - x}};\)
c) \(y = {8^{\frac{x}{3}}};\)
d) \(y = {x^{ - 2}}.\)
Phương pháp giải:
Sử dụng định nghĩa hàm số mũ.
Lời giải chi tiết:
a) \(y = {\left( {\sqrt 2 } \right)^x}\) là hàm số mũ có cơ số là \(\sqrt 2 .\)
b) \(y = {2^{ - x}} = {\left( {{2^{ - 1}}} \right)^x}\) là hàm số mũ có cơ số là \({2^{ - 1}} = \frac{1}{2}.\)
c) \(y = {8^{\frac{x}{3}}} = {\left( {{8^{\frac{1}{3}}}} \right)^x} = {\left( {\sqrt[3]{8}} \right)^x}\) là hàm số mũ có cơ số là \({8^{\frac{1}{3}}} = \sqrt[3]{8} = 2.\)
d) \(y = {x^{ - 2}}\) không là hàm số mũ.
HĐ 2
Cho hàm số mũ \(y = {2^x}.\)
a) Hoàn thành bảng giá trị sau:

b) Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; 2 x ) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị của hàm số
c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số
Phương pháp giải:
Vẽ đồ thị dựa vào các điểm đã lấy sau đó nhìn đồ thị để đưa ra tập giá trị và tính chất biến thiên.
Lời giải chi tiết:
a)

b,
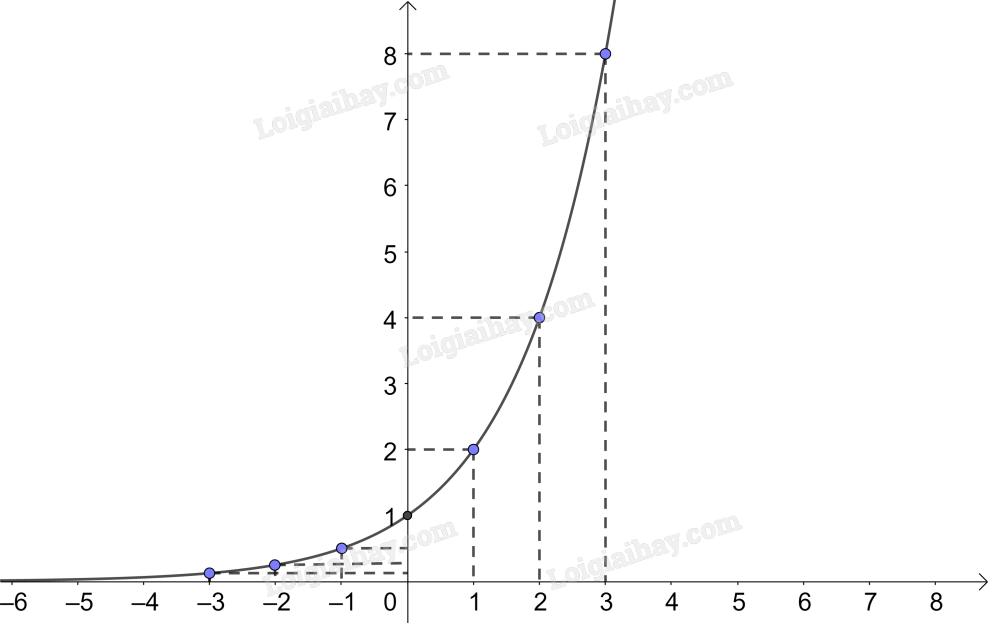
c) Tập giá trị: \(\left( {0; + \infty } \right)\)
Tính chất biến thiên: đồng biến
LT
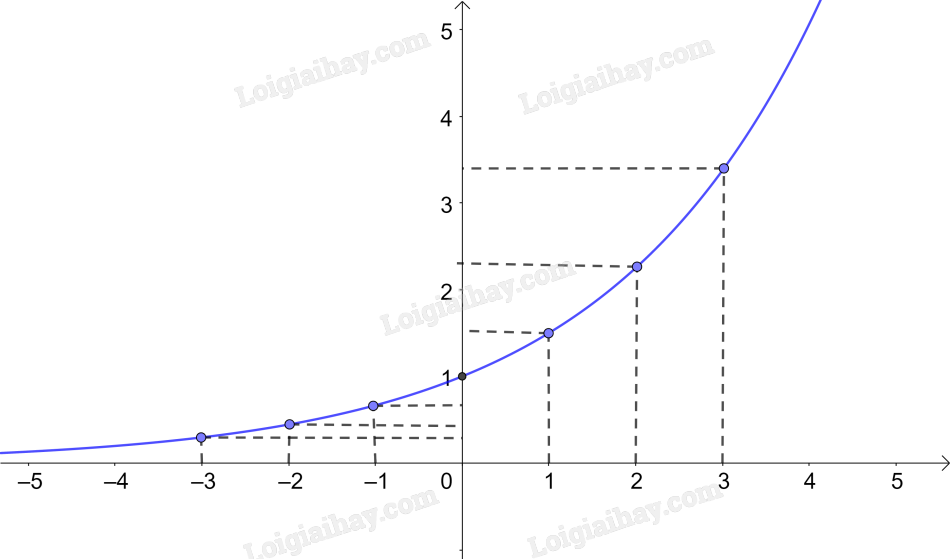
Vẽ đồ thị của hàm số \(y = {\left( {\frac{3}{2}} \right)^x}.\)
Phương pháp giải:
Lập bảng giá trị để vẽ đồ thị hàm số.
Lời giải chi tiết:
Lập bảng giá trị của hàm số tại một điểm như sau:

Từ đó, ta vẽ được đồ thị của hàm số: