Giải mục 1 trang 17,18,19 SGK Toán 12 tập 2 - Cánh diều — Không quảng cáo

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 17 SGK Toán 12 Cánh diều

Cho hàm số $y = f(x) = {x^2}$ (Hình 4). Xét hình phẳng (được tô màu) gồm tất cả điểm M(x;y) trên mặt phẳng tọa độ sao cho $1 \le x \le 2$ và $0 \le y \le {x^2}$. Hình phẳng đó được gọi là hình thang cong AMNB giới hạn bởi đồ thị của hàm số $f(x) = {x^2}$, trục Ox và hai đường thẳng x = 1 và x = 2

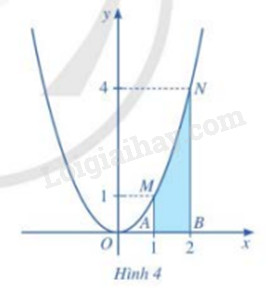
Chia đoạn [1;2] thành n phần bằng nhau bởi các điểm chia: ${x_0} = 1,{x_1} = 1 + \frac{1}{n},{x_2} = 1 + \frac{2}{n},...,{x_{n - 1}} = 1 + \frac{{n - 1}}{n},{x_n} = 1 + \frac{n}{n} = 2$ (Hình 5)

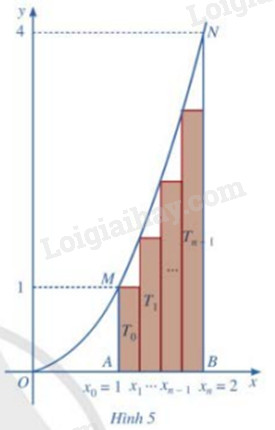
a) Tính diện tích ${T_0}$ của hình chữ nhật dựng trên đoạn $[{x_0};{x_1}]$ với chiều cao là $f({x_0})$

Tính diện tích ${T_1}$ của hình chữ nhật dựng trên đoạn $[{x_1};{x_2}]$ với chiều cao là $f({x_1})$

Tính diện tích ${T_2}$ của hình chữ nhật dựng trên đoạn $[{x_2};{x_3}]$ với chiều cao là $f({x_2})$

…

Tính diện tích ${T_{n - 1}}$ của hình chữ nhật dựng trên đoạn $[{x_{n - 1}};{x_n}]$ với chiều cao là $f({x_{n - 1}})$

b) Đặt ${S_n} = {T_0} + {T_1} + {T_2} + ... + {T_{n - 1}}$. Chứng minh rằng: ${S_n} = \frac{1}{n}[f({x_0}) + f({x_1}) + f({x_2}) + ... + f({x_{n - 1}})]$. Tổng ${S_n}$ gọi là tổng tích phân cấp n của hàm số $f(x) = {x^2}$ trên đoạn [1;2]

Phương pháp giải:

a) Áp dụng công thức tính diện tích hình chữ nhật

b) Biến đổi biểu thức cho thích hợp

Lời giải chi tiết:

a) ${T_0} = f({x_0}).({x_1} - {x_0}) = f(1).({x_1} - 1)$

${T_1} = f({x_1}).({x_2} - {x_1})$

${T_2} = f({x_2}).({x_3} - {x_2})$

…

${T_{n - 1}} = f({x_{n - 1}}).({x_n} - {x_{n - 1}})$ b) ${T_0} = f({x_0}).({x_1} - {x_0}) = f({x_0}).({x_0} + \frac{1}{n} - {x_0}) = \frac{{f({x_0})}}{n}$

${T_1} = f({x_1}).({x_2} - {x_1}) = f({x_1}).({x_1} + \frac{1}{n} - {x_1}) = \frac{{f({x_1})}}{n}$

${T_2} = f({x_2}).({x_3} - {x_2}) = f({x_2}).({x_2} + \frac{1}{n} - {x_2}) = \frac{{f({x_2})}}{n}$

…

${T_{n - 1}} = f({x_{n - 1}}).({x_n} - {x_{n - 1}}) = f({x_{n - 1}}).({x_{n - 1}} + \frac{1}{n} - {x_{n - 1}}) = \frac{{f({x_{n - 1}})}}{n}$

Vậy ${S_n} = {T_0} + {T_1} + {T_2} + ... + {T_{n - 1}} = \frac{1}{n}[f({x_0}) + f({x_1}) + f({x_2}) + ... + f({x_{n - 1}})]$

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 20 SGK Toán 12 Cánh diều

Cho hàm số $f(x) = {x^2}$

a) Chứng tỏ $F(x) = \frac{{{x^3}}}{3}$, $G(x) = \frac{{{x^3}}}{3} + C$ là các nguyên hàm của hàm số $f(x) = {x^2}$

b) Chứng minh rằng $F(b) - F(a) = G(b) - G(a)$, tức là hiệu số $F(b) - F(a)$ không phụ thuộc việc chọn nguyên hàm

Phương pháp giải:

Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x thuộc K

Lời giải chi tiết:

a) $F'(x) = G'(x) = {x^2} = f(x)$ nên $F(x) = \frac{{{x^3}}}{3}$, $G(x) = \frac{{{x^3}}}{3} + C$ là các nguyên hàm của hàm số $f(x) = {x^2}$

b) $F(b) - F(a) = \frac{{{b^3}}}{3} - \frac{{{a^3}}}{3}$

$G(b) - G(a) = \frac{{{b^3}}}{3} + C - \frac{{{a^3}}}{3} - C = \frac{{{b^3}}}{3} - \frac{{{a^3}}}{3}$

=> $F(b) - F(a) = G(b) - G(a)$