Giải mục 1 trang 28,29,30 SGK Toán 12 tập 2 - Cánh diều — Không quảng cáo

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 28 SGK Toán 12 Cánh diều

Cho hàm số $y = f(x) = {x^3} - 2{x^2} - x + 2$ có đồ thị minh họa ở Hình 11.

a) Quan sát Hình 11, hãy cho biết các hình phẳng ${H_1},{H_2},{H_3}$ lần lượt được giới hạn bởi các đường thẳng và đồ thị hàm số nào

b) Tính diện tích ${S_{{H_1}}},{S_{{H_2}}},{S_{{H_3}}}$ của các hình phẳng đó

c) Gọi H là  tập hợp của các hình phẳng ${H_1},{H_2},{H_3}$. Hình phẳng H được gọi là hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và các đường thẳng x = 0, x = 3. Chứng tỏ rằng diện tích ${S_H}$ của hình phẳng H bằng ${S_H} = {S_{{H_1}}} + {S_{{H_2}}} + {S_{{H_3}}} = \int\limits_0^3 {\left| {f(x)} \right|dx}$

Phương pháp giải:

a) Quan sát hình vẽ

b) Sử dụng công thức tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b là: $S = \int\limits_a^b {\left| {f(x)} \right|dx}$

c) Sử dụng tính chất của tích phân $\int\limits_a^b {f(x)} dx = \int\limits_a^c {f(x)} dx + \int\limits_c^b {f(x)} dx$

Lời giải chi tiết:

a) Hình ${H_1}$ được giới hạn bởi các đường thẳng x = 0, x = 1 và đồ thị hàm số y = f(x)

Hình ${H_2}$ được giới hạn bởi các đường thẳng x = 1, x = 2 và đồ thị hàm số y = f(x)

Hình ${H_3}$ được giới hạn bởi các đường thẳng x = 2, x = 3 và đồ thị hàm số y = f(x)

b) ${S_{{H_1}}} = \int\limits_0^1 {f(x)dx}  = \int\limits_0^1 {\left( {{x^3} - 2{x^2} - x + 2} \right)dx}  = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_0^1 = \frac{{13}}{{12}}$

$\int\limits_1^2 {f(x)dx = \int\limits_1^2 {\left( {{x^3} - 2{x^2} - x + 2} \right)} } dx = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_1^2 =  - \frac{5}{{12}} \to {S_{{H_2} = }}\frac{5}{{12}}$

${S_{{H_3}}} = \int\limits_2^3 {f(x)dx = \int\limits_2^3 {\left( {{x^3} - 2{x^2} - x + 2} \right)} } dx = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_2^3 = \frac{{37}}{{12}}$

c) ${S_H} = {S_{{H_1}}} + {S_{{H_2}}} + {S_{{H_3}}} = \int\limits_0^1 {f(x)dx}  + \left| {\int\limits_1^2 {f(x)dx} } \right| + \int\limits_2^3 {f(x)dx}  = \int\limits_0^3 {\left| {f(x)} \right|dx}$

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 30 SGK Toán 12 Cánh diều

Cho các hàm số $y = {2^x}$, y = x

Gọi ${S_1}$ là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số $y = {2^x}$

Gọi ${S_2}$ là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số y = x

Gọi S là phẳng giới hạn bởi các đồ thị hàm số $y = {2^x}$, y = x và hai đường thẳng x = 1, x = 2

(Hình 14)

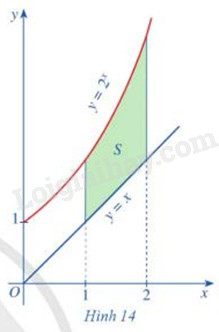
a) Biểu diễn S theo ${S_1},{S_2}$

b) So sánh S và $\int\limits_1^2 {({2^x} - x)dx}$

Phương pháp giải:

Quan sát hình vẽ

Lời giải chi tiết:

a) $S = {S_1} - {S_2}$

b) $S = {S_1} - {S_2}$

$\int\limits_1^2 {({2^x} - x)dx}  = \int\limits_1^2 {{2^x}dx}  - \int\limits_1^2 {xdx}  = {S_1} - {S_2}$

Vậy S = $\int\limits_1^2 {({2^x} - x)dx}$