Giải mục 1 trang 50, 51, 52 SGK Toán 12 tập 2 - Cánh diều — Không quảng cáo

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 50 SGK Toán 12 Cánh diều

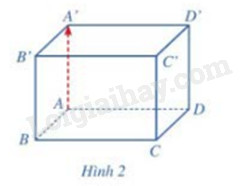
Cho hình hộp chữ nhật ABCD.A’B’C’D’ (Hình 2). Giá của vecto $\overrightarrow {AA'}$ có vuông góc với mặt phẳng (ABCD) hay không?

Phương pháp giải:

Quan sát hình vẽ

Lời giải chi tiết:

Quan sát hình vẽ ta thấy $\overrightarrow {AA'}$ vuông góc với mặt phẳng (ABCD)

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 51 SGK Toán 12 Cánh diều

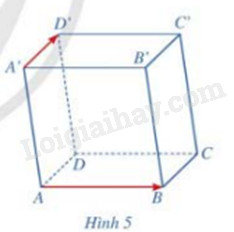
Cho hình hộp ABCD.A’B’C’D’. Cho biết hai vecto $\overrightarrow {AB} ,\overrightarrow {A'D'}$ có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vecto $\overrightarrow {AB} ,\overrightarrow {A'D'}$ và mặt phẳng (ABCD) (Hình 5)

Cho hình hộp ABCD.A’B’C’D’. Cho biết hai vecto $\overrightarrow {AB} ,\overrightarrow {A'D'}$  có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vecto $\overrightarrow {AB} ,\overrightarrow {A'D'}$ và mặt phẳng (ABCD) (Hình 5)

Phương pháp giải:

Quan sát hình vẽ

Lời giải chi tiết:

Hai vecto $\overrightarrow {AB} ,\overrightarrow {A'D'}$  không cùng phương

Giá của vecto $\overrightarrow {AB}$ nằm trong mặt phẳng (ABCD)

Giá của vecto $\overrightarrow {A'D'}$ song song với mặt phẳng (ABCD)

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 52 SGK Toán 12 Cánh diều

Cho cặp vecto chỉ phương $\overrightarrow a  = (1;0;1),\overrightarrow b  = (2;1;0)$ của mặt phẳng (P).

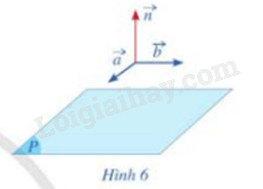
a) Hãy chỉ ra tọa độ của một vecto $\overrightarrow n (\overrightarrow n  \ne \overrightarrow 0 )$ vuông góc với cả hai vecto $\overrightarrow a$ và $\overrightarrow b$ (Hình 6)

b) Vecto $\overrightarrow n$ có là vecto pháp tuyến của mặt phẳng (P) hay không?

Phương pháp giải:

a) Cho hai vecto $\overrightarrow u  = ({x_1};{y_1};{z_1})$ và $\overrightarrow v  = ({x_2};{y_2};{z_2})$ không cùng phương. Khi đó, vecto $\overrightarrow w  = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})$ vuông góc với cả hai vecto $\overrightarrow u$ và $\overrightarrow v$

b) Cho mặt phẳng (P). Nếu vecto $\overrightarrow n$ khác $\overrightarrow 0$ và có giá vuông góc với mặt phẳng (P) thì $\overrightarrow n$ được gọi là vecto pháp tuyến của mặt phẳng ()

Lời giải chi tiết:

a) $\overrightarrow n  = (0.0 - 1.1;1.2 - 0.1;1.1 - 2.0) = ( - 1;2;1)$

b) $\overrightarrow n$ vuông góc với cả hai vecto chỉ phương của mặt phẳng (P) nên $\overrightarrow n$ có giá vuông góc với mặt phẳng (P) và là vecto pháp tuyến của mặt phẳng (P)