Giải mục 1 trang 23, 24 SGK Toán 8 tập 1– Chân trời sáng tạo
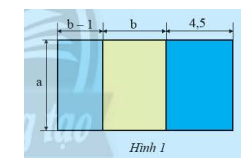
Tính diện tích của nền nhà có bản vẽ sơ lượng như Hình 1 theo những cách khác nhau, biết ; (các kích thước tính theo mét). Tính theo cách nào nhanh hơn?
HĐ1
Tính diện tích của nền nhà có bản vẽ sơ lượng như Hình 1 theo những cách khác nhau, biết \(a = 5\); \(b = 3,5\) (các kích thước tính theo mét). Tính theo cách nào nhanh hơn?
Phương pháp giải:
Áp dụng công thức tính diện tích hình chữ nhật, quy tắc nhân đa thức
Lời giải chi tiết:
Các cách tính diện tích nền nhà là:
Cách 1: \(\left( {b - 1 + b + 4,5} \right)a = \left( {2b + 3,5} \right)a = 2ab + 3,5a\)
Cách 2: \(\left( {b - 1} \right)a + ba + 4,5a = a.\left( {b - 1 + b + 4,5} \right) = a.\left( {2b + 3,5} \right) = 2ab + 3,5a\)
Cách 3: \(\left( {b - 1} \right)a + ba + 4,5a = ba - a + ba + 4,5a = ba + ba - a + 4,5a = 2ab + 3,5a\)
Tính theo cách 1, 2 nhanh hơn
Thực hành 1
Phân tích các đa thức sau thành nhân tử:
a) \(P = 6x - 2{x^3}\)
b) \(Q = 5{x^3} - 15{x^2}y\)
c) \(R = 3{x^3}{y^3} - 6x{y^3}z + xy\)
Phương pháp giải:
Áp dụng phương pháp đặt nhân tử chung.
Lời giải chi tiết:
a) \(P = 6x - 2{x^3}\)\( = 2x.3 - 2x.{x^2} = 2x\left( {3 - {x^2}} \right)\)
b) \(Q = 5{x^3} - 15{x^2}y\)\( = 5{x^2}.x - 5{x^2}.3y = 5{x^2}\left( {x - 3y} \right)\)
c) \(R = 3{x^3}{y^3} - 6x{y^3}z + xy\)\( = xy.3{x^2}{y^2} - xy.6{y^2}z + xy.1 = xy\left( {3{x^2}{y^2} - 6{y^2}z + 1} \right)\)