Giải mục 1 trang 31, 32 SGK Toán 8 tập 1 – Chân trời sáng tạo — Không quảng cáo

HĐ1

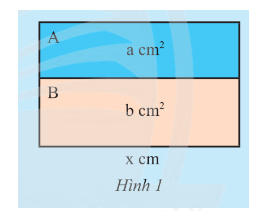
Một hình chữ nhật lớn được ghép bởi hai hình chữ nhật A và B lần lượt có diện tích là \(a\) \(c{m^2}\) và có cùng chiều dài \(x\) cm (Hình 1).

a) Tính chiều rộng của hình chữ nhật lớn theo hai cách khác nhau.

b) Chiều rộng của B lớn hơn chiều rộng của A bao nhiêu? Biết \(b > a\)

Phương pháp giải:

a) Sử dụng kiến thức: Chiều rộng hình chữ nhật bằng diện tích chia cho chiều dài

b) Tính hiệu chiều rộng của hình B và hình A

Lời giải chi tiết:

a) Cách 1: Chiều rộng hình chữ nhật lớn là: \(\left( {a + b} \right):x = \dfrac{{a + b}}{x}\) (cm)

Cách 2: Chiều rộng của hình chữ nhật A là: \(a:x = \dfrac{a}{x}\) (cm)

Chiều rộng của hình chữ nhật B là: \(b:x = \dfrac{b}{x}\) (cm)

Chiều rộng của hình chữ nhật lớn là: \(\dfrac{a}{x} + \dfrac{b}{x} = \dfrac{{a + b}}{x}\) (cm)

b) Chiều rộng của B lớn hơn chiều rộng của A là: \(\dfrac{a}{x} - \dfrac{b}{x} = \dfrac{{a - b}}{x}\) (cm)

Thực hành 1

Thực hiện các phép tính cộng, trừ phân thức sau:

a) \(\dfrac{x}{{x + 3}} + \dfrac{{2 - x}}{{x + 3}}\)               b) \(\dfrac{{{x^2}y}}{{x - y}} - \dfrac{{x{y^2}}}{{x - y}}\)                c) \(\dfrac{{2x}}{{2x - y}} + \dfrac{y}{{y - 2x}}\)

Phương pháp giải:

a) b) Sử dụng quy tắc cộng, trừ hai phân thức có cùng mẫu số

c) Biến đổi hai phân thức thành hai phân thức có cùng mẫu số rồi sử dụng quy tắc cộng, trừ hai phân thức có cùng mẫu số.

Lời giải chi tiết:

a) ĐKXĐ: \(x \ne  - 3\)

\(\dfrac{x}{{x + 3}} + \dfrac{{2 - x}}{{x + 3}}\)\( = \dfrac{{x + 2 - x}}{{x + 3}} = \dfrac{2}{{x + 3}}\)

b) ĐKXĐ: \(x \ne y\)

\(\dfrac{{{x^2}y}}{{x - y}} - \dfrac{{x{y^2}}}{{x - y}}\)\( = \dfrac{{{x^2}y - x{y^2}}}{{x - y}} = \dfrac{{xy\left( {x - y} \right)}}{{x - y}} = xy\)

c) ĐKXĐ: \(2x \ne y\)

\(\dfrac{{2x}}{{2x - y}} + \dfrac{y}{{y - 2x}}\) \( = \dfrac{{2x}}{{2x - y}} - \dfrac{y}{{2x - y}} = \dfrac{{2x - y}}{{2x - y}} = 1\)