Giải mục 1 trang 42, 43 Chuyên đề học tập Toán 10 - Chân trời sáng tạo — Không quảng cáo

HĐ1

Cho elip (E) có phương trình chính tắc $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$ $(0 < b < a)$ và cho điểm $M({x_0};{y_0})$ nằm trên (E). Các điểm ${M_1}( - {x_0};{y_0}),{M_2}({x_0}; - {y_0}),{M_3}( - {x_0}; - {y_0})$ có thuộc (E) hay không?

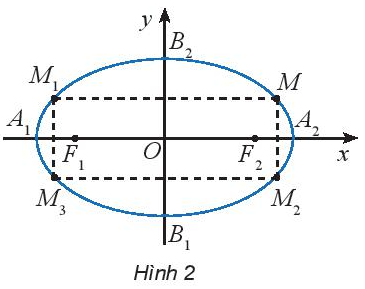
Lời giải chi tiết:

Nếu điểm $M({x_0};{y_0})$ thuộc elip thì $\frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1$

$\Rightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} + \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1$

hay các điểm có tọa độ ${M_1}( - {x_0};{y_0}),{M_2}({x_0}; - {y_0}),{M_3}( - {x_0}; - {y_0})$ cũng thuộc Elip.

Thực hành 1

Viết phương trình chính tắc của elip có kích thước của hình chữ nhật cơ sở là 8 và 6. Hãy xác định tọa độ đỉnh, tiêu điểm, tiêu cự, độ dài trục của elip này.

Phương pháp giải:

Cho elip (E): $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$ $(0 < b < a)$

+ 4 đỉnh là ${A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).$

+ Kích thước của hình chữ nhật cơ sở là 2a và 2b.

+ Tiêu điểm ${F_1}( - c;0),{F_2}(c;0),$

+ Tiêu cự: $2c = 2\sqrt {{a^2} - {b^2}}$

+ Độ dài trục lớn: $2a$, độ dài trục nhỏ: $2b$

Lời giải chi tiết:

Ta có:

+ Kích thước của hình chữ nhật cơ sở là 8 và 6.

$\Rightarrow$ Độ dài trục lớn: $2a = 8 \Leftrightarrow a = 4$, độ dài trục nhỏ: $2b = 6 \Leftrightarrow b = 3$

Phương trình chính tắc của elip là: $\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1$

+ 4 đỉnh là ${A_1}\left( { - 4;0} \right),{A_2}\left( {4;0} \right),{B_1}\left( {0; - 3} \right),{B_2}\left( {0;3} \right).$

+ Tiêu điểm ${F_1}( - c;0),{F_2}(c;0),$

+ Tiêu cự: $2c = 2\sqrt {{4^2} - {3^2}}  = 2\sqrt 7$

+ Độ dài trục lớn: $2a = 8$, độ dài trục nhỏ: $2b = 6$

Vận dụng 1

Hãy gấp một mảnh giấy hình elip (Hình 5) thành 4 phần chồng khít lên nhau

Lời giải chi tiết:

Tưởng tượng elip có phương trình chính tắc trên mặt phẳng tọa độ, khi đó ta chỉ cần gập theo các trục tọa độ.