Giải mục 1 trang 14, 15, 16, 17 Chuyên đề học tập Toán 10 - Chân trời sáng tạo
Ba vận động viên Hùng, Dũng và Mạnh tham gia thi đấu nội dung ba môn phối hợp: chạy, bơi và đạp xe, trong đó tốc độ trung bình của họ trên mỗi chặng đua được cho ở bảng dưới đây.
Đề bài
Thực hành 1 trang 14
Ba vận động viên Hùng, Dũng và Mạnh tham gia thi đấu nội dung ba môn phối hợp: chạy, bơi và đạp xe, trong đó tốc độ trung bình của họ trên mỗi chặng đua được cho ở bảng dưới đây.
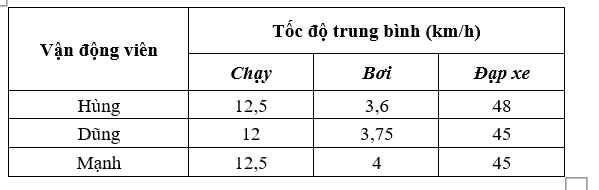
Biết tổng thời gian thi đấu ba môn phối hợp của Hùng là 1 giờ 1 phút 30 giây, của Dũng là 1 giờ 3 phút 40 giây và của Mạnh là 1 giờ 1 phút 55 giây. Tính cự li của mỗi chặng đua.
Lời giải chi tiết
Gọi cự li của mỗi chặng đua chạy, bơi và đạp xe là x, y, z (đơn vị km) (\(x, y, z > 0\)).
Thời gian = Cự li : Vận tốc.
Tổng thời gian thi đấu ba môn phối hợp của Hùng là 1 giờ 1 phút 30 giây = 1,025 giờ, nên ta có:
\(\frac{x}{{12,5}} + \frac{y}{{3,6}} + \frac{z}{{48}} = 1,025\)
Tổng thời gian thi đấu ba môn phối hợp của Dũng là 1 giờ 3 phút 40 giây = \(\frac{{191}}{{180}}\)giờ, nên ta có:
\(\frac{x}{{12}} + \frac{y}{{3,75}} + \frac{z}{{45}} = \frac{{191}}{{180}}\)
Tổng thời gian thi đấu ba môn phối hợp của Mạnh là 1 giờ 1 phút 55 giây = \(\frac{{743}}{{720}}\)giờ, nên ta có:
\(\frac{x}{{12,5}} + \frac{y}{4} + \frac{z}{{45}} = \frac{{743}}{{720}}\)
Từ đó ta có hệ phương trình bậc nhất ba ẩn
\(\left\{ \begin{array}{l}\frac{x}{{12,5}} + \frac{y}{{3,6}} + \frac{z}{{48}} = 1,025\\\frac{x}{{12}} + \frac{y}{{3,75}} + \frac{z}{{45}} = \frac{{191}}{{180}}\\\frac{x}{{12,5}} + \frac{y}{4} + \frac{z}{{45}} = \frac{{743}}{{720}}\end{array} \right.\)
Sử dụng máy tính cầm tay, ta được \(x = 5;y = 0,75;z = 20\).
Vậy cự li chạy là 5km, cự li bơi là 0,75km và cự li đạp xe là 20km.