Giải mục 1 trang 65, 66, 67 SGK Toán 10 tập 1 - Chân trời sáng tạo
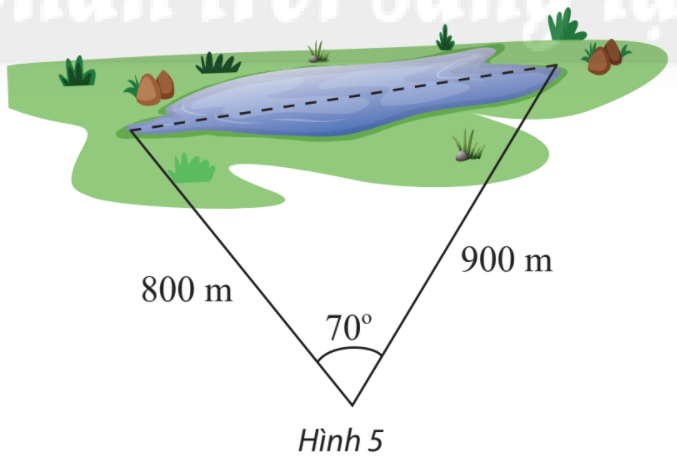
Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 880 m và 900 m người quan sát nhìn hai điểm này dưới một góc 70 (Hình 5).
HĐ Khởi động
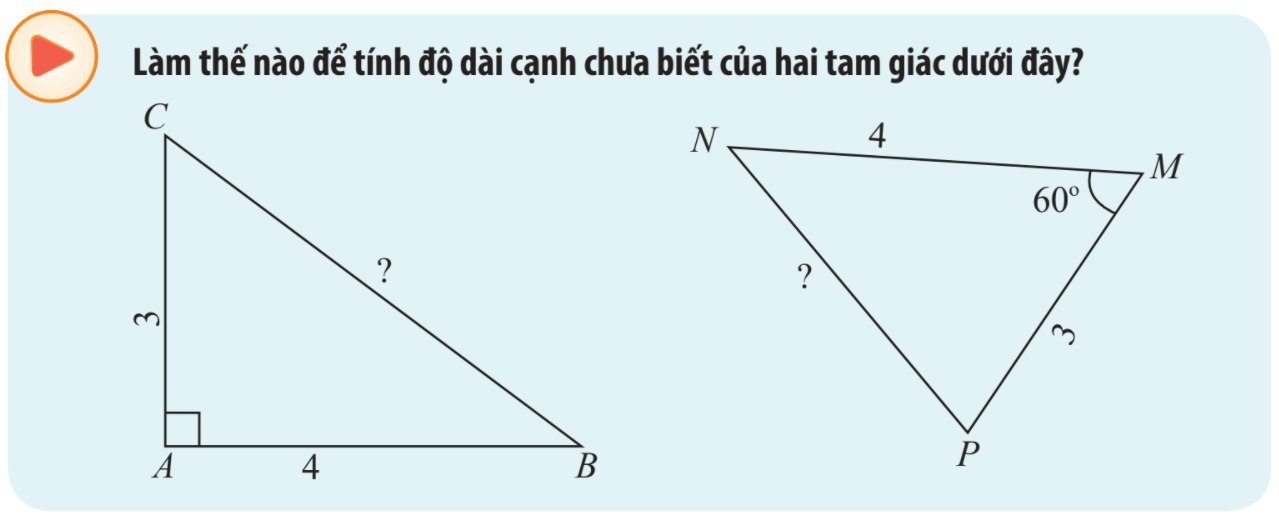
Phương pháp giải:
Với \(\widehat A = {90^o}\) ta sử dụng định lí Pytago.
Với \(\widehat A \ne {90^o}\): Áp dụng định lí cosin: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lời giải chi tiết:
Áp dụng định lí Pytago, ta có:
\(\begin{array}{l}B{C^2} = A{C^2} + A{B^2} = {3^2} + {4^2} = 25\\ \Rightarrow BC = 5\end{array}\)
Áp dụng định lí cosin trong tam giác MNP, ta có:
\(N{P^2} = M{N^2} + M{P^2} - 2.MN.MP\cos M\)
Mà \(MN = 4,MP = 3,\widehat M = {60^o}\)
\(\begin{array}{l} \Rightarrow N{P^2} = {4^2} + {3^2} - 2.4.3\cos {60^o} = 13\\ \Leftrightarrow NP = \sqrt {13} \approx 3,6\end{array}\)
HĐ Khám phá 1
a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và \(\widehat C \ge \widehat B.\) Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.
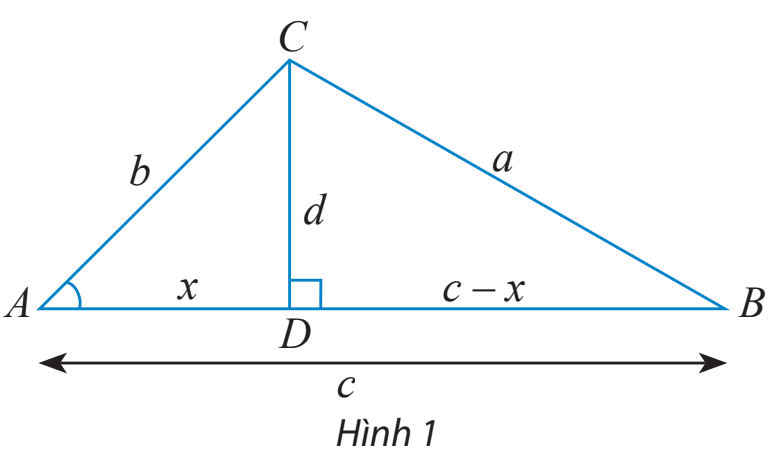
Hãy thay ? bằng các chữ cáu thích hợp để chứng minh công thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) theo gợi ý sau:
Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c - x)^2} = {d^2} + {x^2} + {c^2} - 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = \frac{?}{b} \Rightarrow ? = b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lưu ý : Nếu \(\widehat B > \widehat C\) thì ta vẽ đường cao BD và chứng minh tương tự.
b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
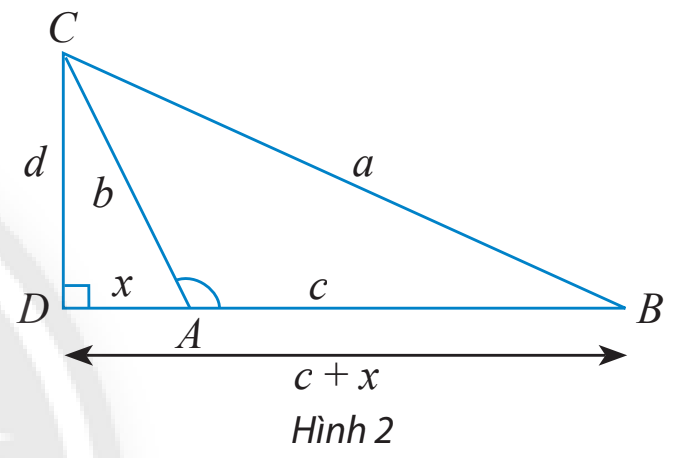
Lưu ý : Vì A là góc tù nên \(\cos A = - \frac{x}{b}.\)
c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ coogn thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) có thể viết là \({a^2} = {b^2} + {c^2}.\)
Lời giải chi tiết:
a) ? = x vì \(\cos A = \frac{{AD}}{{AC}} = \frac{x}{b} \Rightarrow ? = x.\)
b) Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c + x)^2} = {d^2} + {x^2} + {c^2} + 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = - \cos \widehat {DAC} = - \frac{x}{b} \Rightarrow x = - b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
c) Ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Mà \(\widehat A = {90^o} \Rightarrow \cos A = \cos {90^o} = 0.\)
\( \Rightarrow {a^2} = {b^2} + {c^2}\)
Thực hành 1
Tính các cạnh và các góc chưa biết của tam giác ABC trong hình 4.
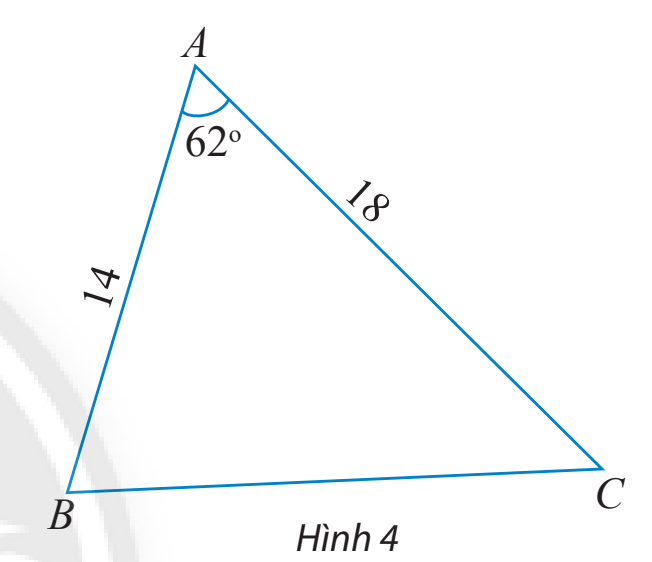
Phương pháp giải:
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\\\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}};\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}}\end{array}\)
Lời giải chi tiết:
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
Mà \(AB = 14,AC = 18,\widehat A = {62^o}\)
\(\begin{array}{l} \Rightarrow B{C^2} = {18^2} + {14^2} - 2.18.14\cos {62^o} \approx 283,3863\\ \Leftrightarrow BC \approx 16,834\end{array}\)
Lại có: Từ định lí cosin ta suy ra:
\(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}};\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}}\)
\( \Rightarrow \left\{ \begin{array}{l}\cos B = \frac{{{{14}^2} + 16,{{834}^2} - {{18}^2}}}{{2.14.16,834}} \approx 0,3297\\\cos C = \frac{{{{18}^2} + 16,{{834}^2} - {{14}^2}}}{{2.18.16,834}} \approx 0,6788\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat B \approx {70^o}45'\\\widehat C \approx {47^o}15'\end{array} \right.\)
Vậy \(BC \approx 16,834;\widehat B \approx {70^o}45';\widehat C \approx {47^o}15'.\)
Vận dụng 1
Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 800 m và 900 m người quan sát nhìn hai điểm này dưới một góc \({70^o}\) (Hình 5).
Phương pháp giải:
Áp dụng định lí cosin \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lời giải chi tiết:
Kí hiệu hai vị trí đầu hồ và vị trí quan sát lần lượt bở các điểm A, B, C như hình dưới:
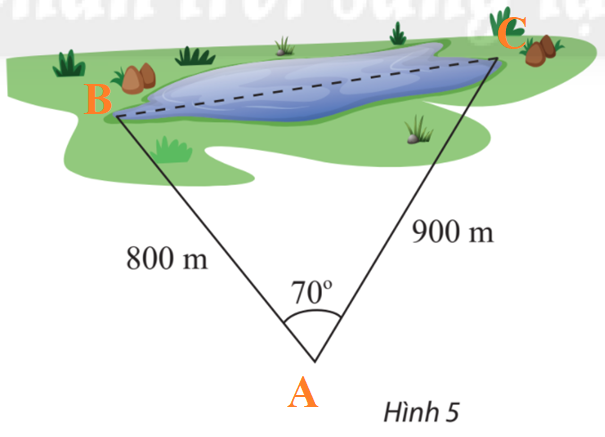
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
Mà \(AB = 800,AC = 900,\widehat A = {70^o}\)
\(\begin{array}{l} \Rightarrow B{C^2} = {900^2} + {800^2} - 2.900.800\cos {70^o} \approx 957490,9936\\ \Leftrightarrow BC \approx 978,5147\end{array}\)
Vậy khoảng cách giữa hai điểm ở hai đầu hồ là 978,5147 m.