Giải mục 2 trang 29, 30 SGK Toán 11 tập 2 - Kết nối tri thức
Đối với hai cánh cửa trong Hình 7.5, tính góc giữa hai đường mép cửa BC và MN
HĐ2
Đối với hai cánh cửa trong Hình 7.5, tính góc giữa hai đường mép cửa BC và MN

Phương pháp giải:
Để xác định góc giữa hai đường thẳng chéo nhau a và b, ta có thể lấy một điểm O thuộc đường thẳng a và qua đó kẻ đường thẳng b' song song với b. Khi đó (a, b) = (a', b')
Lời giải chi tiết:
Vì BC // PN nên (BC, MN) = (PN, MN)
Mà PN vuông góc với MN nên góc giữa hai đường mép này bằng 90 0 .
CH
Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b hay không?
Phương pháp giải:
\(\left. \begin{array}{l}a \bot b\\b//c\end{array} \right\} \Rightarrow a \bot c\)
Lời giải chi tiết:
Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b.
LT1
Cho tam giác MNP vuông tại N và một điểm A nằm ngoài mặt phẳng (MNP). Lần lượt lấy các điểm B, C, D sao cho M, N, P tương ứng là trung điểm của AB, AC, CD (H.7.7). Chứng minh rằng AD và BC vuông góc với nhau và chéo nhau.
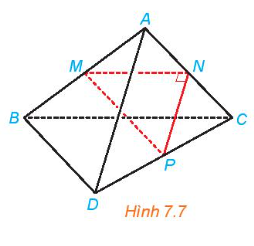
Phương pháp giải:
Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b.
Lời giải chi tiết:
+) Xét tam giác ABC có
M, N lần lượt là trung điểm của AB, AC
\( \Rightarrow \) MN là đường trung bình của tam giác ABC
\( \Rightarrow \) MN // BC
Mà NP \( \bot \) MN nên NP \( \bot \) BC
Xét tam giác ADC có
N, P lần lượt là trung điểm của AC, CD
\( \Rightarrow \) PN là đường trung bình của tam giác ADC
\( \Rightarrow \) PN // AD
Mà NP \( \bot \) BC nên AD \( \bot \) BC
+) BC // MN mà \(MN \subset \left( {MNP} \right) \Rightarrow BC//\left( {MNP} \right)\)
PN // AD mà \(PN \subset \left( {MNP} \right) \Rightarrow AD//\left( {MNP} \right)\)
Vậy AD và BC chéo nhau.