Giải mục 2 trang 63, 64, 65 SGK Toán 8 - Cùng khám phá
Cắt hình bình hành ABCD theo đường chéo AC
Hoạt động 1
Cắt hình bình hành ABCD theo đường chéo AC và xếp chồng tam giác CDA lên tam giác ABC như nhình 3.28. Em hãy nhận xét về cạnh và góc của hai tam giác.
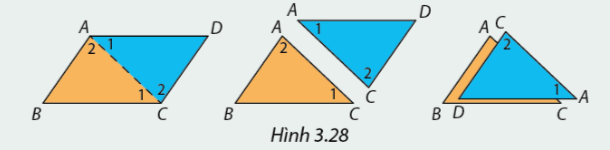
Sử dụng tính chất của hai đường thẳng song song, em hãy cho biết vì sao \(\widehat {{A_1}} = \widehat {{C_1}}\) và \(\widehat {{A_2}} = \widehat {{C_2}}\), từ đó giải thích vì sao \(\Delta ABC = \Delta CDA?\) Em có kết luận gì về độ dài các cặp cạnh \(AB\) và \(CD,\)\(BC\)và \(AD\), số đo cặp góc \(\widehat B\) và \(\widehat D?\)
Phương pháp giải:
Sử dụng tính chất của hai đường thẳng song song suy ra \(\widehat {{A_1}} = \widehat {{C_1}}\) và \(\widehat {{A_2}} = \widehat {{C_2}}\)
Từ đó suy ra \(\Delta ABC = \Delta CDA.\)
Các cặp góc, cặp cạnh tương ứng bằng nhau.
Lời giải chi tiết:
Có \(AD//BC\) nên \(\widehat {{A_1}} = \widehat {{C_1}}\) (so le trong).
Tương tự có \(AB//DC \Rightarrow \widehat {{A_2}} = \widehat {{C_2}}\) (so le trong)
Xét tam giác ABC và tam giác CDA có
\(\widehat {{A_1}} = \widehat {{C_1}}\)
\(AC\) chung
\(\widehat {{A_2}} = \widehat {{C_2}}\)
Vậy \(\Delta ABC = \Delta CDA\left( {g - c - g} \right)\)\( \Rightarrow AB = CD;BC = AD\)(hai cạnh tương ứng)
\(\widehat B = \widehat D\) (hai góc tương ứng).
Hoạt động 2
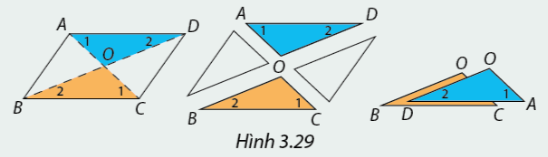
Cắt hình bình hành ABCD theo đường chéo AC, BD và xếp chồng tam giác OAD lên tam giác OCB như Hình 3.29. Em có nhận xét gì về cạnh và góc của hai tam giác?
Phương pháp giải:
Sử dụng tính chất song song, chứng minh \(\Delta OAD = \Delta OCB\left( {g - c - g} \right)\)
Suy ra các cặp cạnh, cặp góc tương ứng bằng nhau.
Lời giải chi tiết:
Ta thấy \(AD//BC \Rightarrow \widehat {{A_1}} = \widehat {{C_1}};\widehat {{A_2}} = \widehat {{C_2}}.\)
Mà \(AD = BC\) nên \(\Delta OAD = \Delta OCB\left( {g - c - g} \right)\)
Hai tam giác có các cặp cạnh tương ứng bằng nhau, các cặp góc tương ứng bằng nhau.
Luyện tập 1
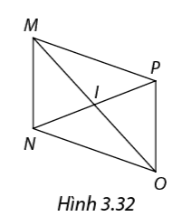
Trong hình 3.32, MONP là hình bình hành có MO và NP cắt nhau tại I và \(IN = 3cm,IO = 4cm,ON = 6cm.\) Tìm độ dài cạnh MP và đường chéo MO, NP.
Phương pháp giải:
Sử dụng định lí của hình bình hành.
Trong hình bình hành:
a) Các cạnh đối bằng nhau;
b) Các góc đối bằng nhau;
c) Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết:
Xét hình bình hành MNOP có \(MP = ON = 6cm.\)
I là giao điểm của MO và NP suy ra I là trung điểm của mỗi đường.
\( \Rightarrow IN = IP = 3cm;IO = IM = 4cm\)
\(NP = 2IN = 6cm;MO = 2IO = 8cm.\)