Giải mục 2 trang 68, 69 SGK Toán 8 - Cùng khám phá
Trong Hình 3.42, giải thích vì sao
Hoạt động 1
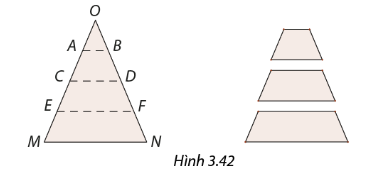
Trong Hình 3.42 , giải thích vì sao \(\Delta OAB\) và \(\Delta OCD\) là các tam giác cân tại O. Em hãy so sánh các cặp cạnh \(OA\) và \(OB,OC\) và \(OD\). Từ đó có thể kết luận gì về hai đoạn thẳng \(AC\) và \(BD\)?
Phương pháp giải:
Dựa vào tính chất tam giác cân và tính chất hình thang cân để giải thích.
Lời giải chi tiết:
Ta có \(CD//MN\) nên tam giác \(OCD\) là tam giác cân. Chứng minh tương tự với tam giác \(OAB\).
Ta thấy vì tam giác \(OAB\) là tam giác cân nên có cạnh \(OA = OB\).
Tam giác \(OCD\) là tam giác cân nên có cạnh \(OC = OD\)
\( = > AC = BD\)
Luyện tập 2
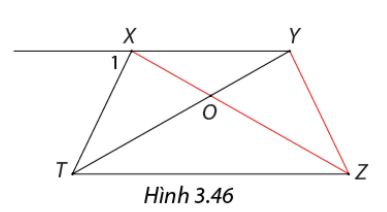
Trong Hình 3.46 , cho \(\widehat {{X_1}} = \widehat {XTZ} = \widehat {YZT},XT = 6,OT = 7\) và \(OY = 4\). Tứ giác \(XYZT\) là hình gì? Tìm độ dài \(XZ\) và \(YZ\).
Phương pháp giải:
Dựa vào tính chất của hình thang cân: Trong hình thang cân hai cạnh bên bằng nhau và hai đường chéo bằng nhau.
Lời giải chi tiết:
Xét tứ giác \(XYZT\), ta có:
\(\widehat {{X_1}} = \widehat {XTZ}\)
Mà hai góc này ở vị trí so le trong
=> \(XY//TZ\)
=> Tứ giác \(XYZT\) là hình thang
Lại có:
\(\widehat {XTZ} = \widehat {YZT}\)
Mà hai góc này là hai góc kề đáy \(TZ\)
=> Tứ giác \(XYZT\) là hình thang cân
Trong tam giác cân hai đường chéo bằng nhau
=> \(XZ = YT = 7 + 4 = 11\)
Trong tam giác cân hai cạnh bên bằng nhau
=> \(XT = YZ = 6\)