Giải mục 3 trang 106, 107 SGK Toán 8 tập 1 - Cánh diều
a) Cho tứ giác ABCD có AB = CD, BC = DA (hình 39) - Hai tam giác ABC và CDA có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc: (widehat {BAC}) và (widehat {DCA};widehat {ACB}) và (widehat {C{rm{D}}A}). ABCD có phải là hình bình hành hay không?
HĐ3
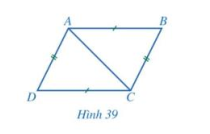
a) Cho tứ giác ABCD có AB = CD, BC = DA (hình 39)
- Hai tam giác ABC và CDA có bằng nhau hay không?
Từ đó, hãy so sánh các cặp góc: \(\widehat {BAC}\) và \(\widehat {DCA};\widehat {ACB}\) và \(\widehat {CAD}\).
ABCD có phải là hình bình hành hay không?
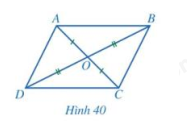
b) Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường (Hình 40)
Hai tam giác ABO và CDO có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc: \(\widehat {BAC}\) và \(\widehat {DCA};\widehat {ACB}\) và \(\widehat {CA{\rm{D}}}\).
ABCD có phải là hình bình hành hay không?
Phương pháp giải:
Chứng minh các tam giác bằng nhau từ đo suy ra các cạnh và các góc tương ứng bằng nhau.
Lời giải chi tiết:
a) Xét hai tam giác ABC và CDA có:AB = CD; AD = BC; AC chung nên \(\Delta ABC = \Delta C{\rm{D}}A(c - c - c)\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CAD}\).
Nên ABCD hình bình hành.
b) Xét hai tam giác ABO và tam giác CDO có: \(OA = OB;\widehat {AOB} = \widehat {CO{\rm{D}}};OC = O{\rm{D}}\)
Suy ra: \(\Delta ABO = \Delta C{\rm{D}}O\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CA{\rm{D}}}\).
Nên ABCD là hình bình hành.
LT2
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thỏa mãn: OA = OC và \(\widehat {OA{\rm{D}}} = \widehat {OCB}\). Chứng minh tứ giác ABCD là hình bình hành.
Phương pháp giải:
Chứng minh tứ giác ABCD có: OA = OC; OB = OD
Lời giải chi tiết:
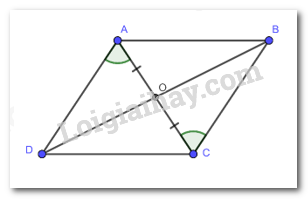
Xét tam giác AOD và tam giác COB có:
\(\begin{array}{l}OA = OC\\\widehat {DAO} = \widehat {BCO}(gt)\\\widehat {AO{\rm{D}}} = \widehat {BOC}(gt)\\ \Rightarrow \Delta AO{\rm{D}} = \Delta COB\\ \Rightarrow O{\rm{D}} = OB\end{array}\)
Tứ giác ABCD có OA = OC; OB = OD nên tứ giác ABCD là hình bình hành.