Giải mục 3 trang 115 SGK Toán 8 tập 1 - Cánh diều
a) Cho hình bình hành ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình thoi hay không? b) Cho hình bình hành ABCD có hai đường chéo AC và BD vuông góc với nhau (hình 60) - Đường thẳng AC có phải là đường trung trực của đoạn thẳng BD hay không? ABCD có phải là hình thoi hay không?
HĐ3
a) Cho hình bình hành ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình thoi hay không?
b) Cho hình bình hành ABCD có hai đường chéo AC và BD vuông góc với nhau (hình 60)
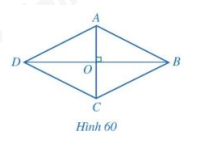
- Đường thẳng AC có phải là đường trung trực của đoạn thẳng BD hay không?
ABCD có phải là hình thoi hay không?
Phương pháp giải:
Hình thoi là tứ giác có 4 cạnh bằng nhau.
Lời giải chi tiết:
a) Hình bình hành ABCD có AB = BC
Suy ra: AB = BC = CD = DA
Nên hình bình hành ABCD là hình thoi
b) AC giao điểm với BD tại O
Ta có: O là trung điểm của BD (do ABCD là hình bình hành)
AO vuông góc với BD
Suy ra AO là đường trung trực của đoạn thẳng BD
Suy ra tam giác ABD cân tại A
Suy ra: AB = AD
Suy ra AB = DC = AD = BC
Hình bình hành ABCD là hình thoi
LT2
Cho tam giác ABC cân tại A có M là trung điểm BC. Trên tia đối của tia MA lấy điểm N sao cho MN = MA. Chứng minh tứ giác ABNC là hình thoi.
Phương pháp giải:
Chứng minh tứ giác ABNC là hình bình hành có AB = AC
Lời giải chi tiết:
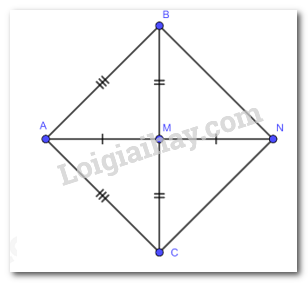
Tứ giác ABNC có: M là giao điểm của AN và BC
MN = MA
MB = MC (do M là trung điểm của BC)
Suy ra: tứ giác ABNC là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
Mà: AB = AC (do tam giác ABC cân tại A)
Suy ra: hình bình hành ABNC là hình thoi (Hình bình hành có 2 cạnh kề bằng nhau)