Giải mục 3 trang 110,111 SGK Toán 8 tập 1 - Cánh diều
a) Cho hình bình hành ABCD có (widehat A = {90^o}). ABCD có phải là hình chữ nhật hay không? b) Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (hình 50) Hai tam giác ABC và DCB có bằng nhau hay không? Từ đó, hãy so sánh (widehat {ABC}) và (widehat {DCB}). ABCD có phải là hình chữ nhật hay không?
HĐ3
a) Cho hình bình hành ABCD có \(\widehat A = {90^o}\). ABCD có phải là hình chữ nhật hay không?
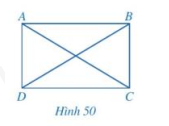
b) Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (hình 50)
Hai tam giác ABC và DCB có bằng nhau hay không? Từ đó, hãy so sánh \(\widehat {ABC}\) và \(\widehat {DCB}\).
ABCD có phải là hình chữ nhật hay không?
Phương pháp giải:
Vận dụng các tính chất của hình bình hành
Lời giải chi tiết:
a) Hình bình hành ABCD có \(\widehat A = {90^o}\)
Suy ra: \(\widehat C = \widehat A = {90^o}\)
Suy ra: \(\widehat B = \widehat D = \dfrac{{{{360}^o} - \widehat A - \widehat C}}{2} = \dfrac{{{{360}^o} - {{90}^o} - {{90}^o}}}{2} = {90^o}\)
Vậy ABCD là hình chữ nhật
b) Xét hai tam giác ABC và tam giác DCB có:
BC chung
AB = DC
AC = BD
Suy ra: \(\Delta ABC = \Delta DCB \Rightarrow \widehat {ABC} = \widehat {DCB}\)
Suy ra: \(\widehat {ABC} = \widehat {DCB} = \widehat {ADC} = \widehat {DAB} = {360^o}:4 = {90^o}\)
Vậy ABCD là hình chữ nhật.
LT2
Cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O thỏa mãn \(\widehat {OAB} = \widehat {O{\rm{D}}C}\). Chứng minh ABCD là hình chữ nhật.
Phương pháp giải:
Chứng minh hình bình hành ABCD có AC = BD.
Lời giải chi tiết:
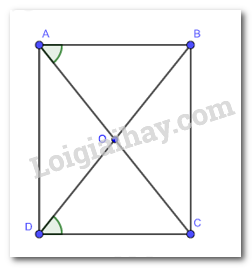
Do ABCD là hình bình hành suy ra AB = CD và AB // CD nên \(\widehat{ABO}=\widehat{ODC}\) (hai góc so le trong\)
Mà \(\widehat {OAB} = \widehat {O{\rm{D}}C}\) nên \(\widehat{ABO}=\widehat{OAB}\) suy ra tam giác AOB cân tại O.
Vì tam giác AOB cân tại O nên OA = OB.
Mà hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường nên AC = BD.
Suy ra ABCD có hai đường chéo AC = BD nên ABCD là hình chữ nhật.