Giải mục 3 trang 28 SGK Toán 12 tập 1 - Cùng khám phá
Khảo sát sự biến thiên và vẽ đồ thị của hàm số (y = f(x) = frac{{2x + 4}}{{2x + 1}}).
LT2
Trả lời câu hỏi Luyện tập 2 trang 28 SGK Toán 12 Cùng khám phá
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = f(x) = \frac{{2x + 4}}{{2x + 1}}.\)
Phương pháp giải:
- Tìm tập xác định của hàm số.
- Xét sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.
Lời giải chi tiết:
- Tập xác định: \({\rm{D}} = {\rm{R}}\backslash \left\{ {\frac{{ - 1}}{2}} \right\}\).
- Sự biến thiên:
Giới hạn, tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 4}}{{2x + 1}} = 1.\)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x + 4}}{{2x + 1}} = 1.\)
Suy ra đường thẳng \({\rm{y}} = 1\) là đường tiệm cận ngang của đồ thị hàm số đã cho
\(\mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ + }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ + }} \frac{{2x + 4}}{{2x + 1}} = + \infty \)
\(\mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ - }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ - }} \frac{{2x + 4}}{{2x + 1}} = - \infty \)
Suy ra đường thẳng \({\rm{x}} = \frac{{ - 1}}{2}\). là đường tiệm cận đứng của đồ thị hàm số đã cho
Ta có: \({y^\prime } = \frac{{ - 6}}{{{{(2x + 1)}^2}}} < 0.\)
Suy ra hàm số nghịch biến trên tập xác định.
Bảng biến thiên:
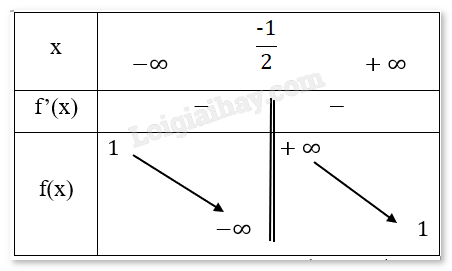
Chiều biến thiên: Hàm số nghịch biến trên \(\left( { - \infty ,\frac{{ - 1}}{2}} \right)\) và \(\left( {\frac{{ - 1}}{2}, + \infty } \right)\)
Cực trị: Hàm số không có cực trị.
- Vẽ đồ thị:
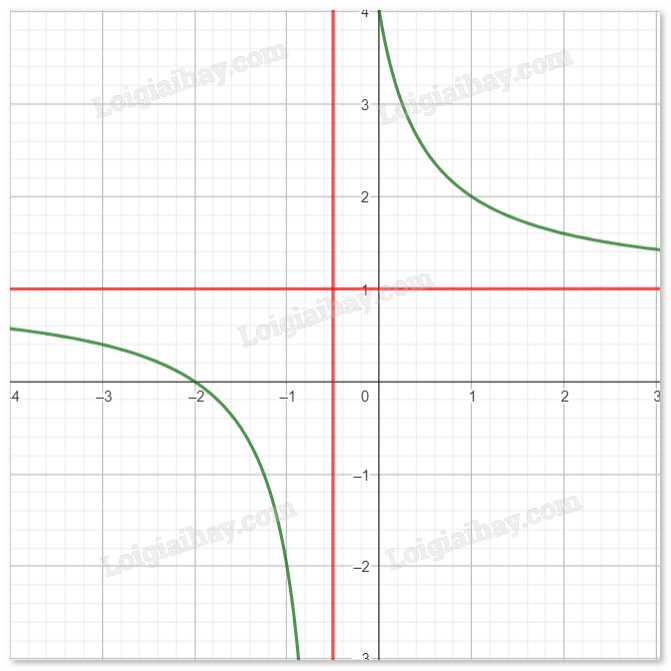
VD2
Trả lời câu hỏi Vận dụng 2 trang 28 SGK Toán 12 Cùng khám phá
Ở một bể chứa nước có chứa 1000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít vào bể nước với tốc độ là 25 lít/phút.
a) Chứng minh rằng nồng độ muối của nước trong bể sau t phút kể từ khi bắt đầu bơm là: \(C(t) = \frac{{30t}}{{40 + t}}.\)
b) Khảo sát sự biến thiên của hàm số \(y = C(t)\) sau 10 tiếng kể từ lúc bắt đầu bơm, từ đó nhận xét về nồng độ muối trong bể khi thời gian ttt càng lớn.
Phương pháp giải:
a)
Tính lượng nước biển bơm vào sau 𝑡 phút.
Tính tổng lượng nước trong bể sau 𝑡 phút.
Tính lượng muối bơm vào bể sau 𝑡 phút.
Tính nồng độ muối 𝐶(𝑡).
b)
Tính giới hạn của C(t) khi \(t \to \infty \) .
Tính đạo hàm của C(t).
Xét dấu của đạo hàm C’(t).
Từ dấu của đạo hàm và giới hạn khi \(t \to \infty \)kết luận về sự biến thiên và giá trị tiệm cận của hàm số.
Lời giải chi tiết:
a)
Lượng nước biển bơm vào sau \(t\) phút: \(V = 25t\) lít.
Tổng lượng nước trong bể sau \(t\) phút: \(1000 + 25t\) lít.
Lượng muối bơm vào bể sau \(t\) phút: \(30.25t = 750t {\rm{gam}}.\)
Nồng độ muối \(C(t) = \frac{{750t}}{{1000 + 25t}} = \frac{{750t}}{{25(40 + t)}} = \frac{{30t}}{{40 + t}}.\)
b)
Vì t là thời gian nên tập xác định của hàm số
\({\rm{y}} = C(t)\) là t > 0.
Giới hạn của \(C(t)\) khi \(t \to \infty \) : \(\mathop {\lim }\limits_{t \to \infty } \frac{{30t}}{{40 + t}} = 30.\)
Đạo hàm của \(C(t)\) : \({C^\prime }(t) = \frac{{30.(40 + t) - 30t.1}}{{{{(40 + t)}^2}}} = \frac{{1200 + 30t - 30t}}{{{{(40 + t)}^2}}} = \frac{{1200}}{{{{(40 + t)}^2}}}.\)
Nhận thấy \({C^\prime }(t) > 0\forall t > 0.\)
Vậy nồng độ muối trong bể tăng dần khi thời gian \(t\) càng lớn.
Khi \(t \to \infty \), nồng độ muối trong bể tiệm cận 30 gam/lít.