Giải mục 3 trang 60, 61, 62, 63, 64 SGK Toán 12 tập 1 - Cùng khám phá
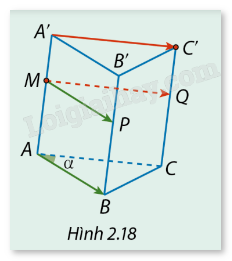
Cho hình lăng trụ ABC.A'B'C' có \(\widehat {BAC} = \alpha \). Gọi M là một điểm bất kỳ thuộc cạnh bên AA' (Hình 2.18). a) Vẽ hai vectơ \(\overrightarrow {MP} \) và \(\overrightarrow {MQ} \) lần lượt bằng \(\overrightarrow {AB} \) và \(\overrightarrow {A'C'} \). ABC.MPQ có phải là hình lăng trụ không? Vì sao? b) Trong mặt phẳng (MPQ), hãy xác định góc giữa hai vectơ \(\overrightarrow {MP} \), \(\overrightarrow {MQ} \) và so sánh góc đó với \(\alpha \).
LT5
Trả lời câu hỏi Luyện tập 5 trang 60 SGK Toán 12 Cùng khám phá
Cho hình lăng trụ ABC.A'B'C' có \(\widehat {BAC} = \alpha \). Gọi M là một điểm bất kỳ thuộc cạnh bên AA' (Hình 2.18).
a) Vẽ hai vectơ \(\overrightarrow {MP} \) và \(\overrightarrow {MQ} \) lần lượt bằng \(\overrightarrow {AB} \) và \(\overrightarrow {A'C'} \). ABC.MPQ có phải là hình lăng trụ không? Vì sao?
b) Trong mặt phẳng (MPQ), hãy xác định góc giữa hai vectơ \(\overrightarrow {MP} \), \(\overrightarrow {MQ} \) và so sánh góc đó với \(\alpha \).
Phương pháp giải:
- Sử dụng định nghĩa và tính chất của vectơ kết hợp với khái niệm và các tính chất của hình lăng trụ.
- Hình lăng trụ là hình đa diện bao gồm 2 đáy nằm trên hai mặt phẳng song song và là hai đa giác bằng nhau.
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {MP} = \overrightarrow {AB} \) suy ra MP = AB và MP // AB (1)
Tương tự: \(\overrightarrow {MQ} = \overrightarrow {A'C'} \) suy ra MQ = A’C’ = AC và MQ // A’C’ // AC (2)
Từ (1) và (2) suy ra \(\Delta MPQ = \Delta ABC\).
ABC.MPQ có hai đáy song song và bằng nhau nên ABC.MPQ là hình lăng trụ.
b) Vì \(\Delta MPQ = \Delta ABC\) nên \(\widehat {PMQ} = \widehat {BAC} = \alpha \).
Mà góc giữa hai vectơ \(\overrightarrow {MP} \) và \(\overrightarrow {MQ} \) là góc\(\widehat {PMQ}\).
Vậy \(\widehat {(\overrightarrow {MP} ,\overrightarrow {MQ} )} = \alpha \).
LT6
Trả lời câu hỏi Luyện tập 6 trang 61 SGK Toán 12 Cùng khám phá
Cho hình lập phương \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và
a) vecto \(\overrightarrow {AB} \);
b) vectơ \(\overrightarrow {AD} \);
c) vectơ \(\overrightarrow {{B^\prime }B} \).
Phương pháp giải:
Sử dụng các tính chất của hình lập phương để xác định góc của các vectơ.
Lời giải chi tiết:
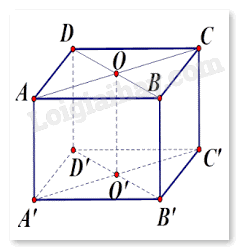
Gọi độ dài cạnh của hình lập phương là \(a\).
a) Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và vectơ \(\overrightarrow {AB} \):
Vì ABCD.A’B’C’D’ là hình lập phương nên \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} \).
Mà góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {AB} \) là \(\widehat {BAC}\) và vì ABCD là hình vuông nên \(\widehat {BAC} = 45^\circ \).
Suy ra \(\widehat {(\overrightarrow {A'C'} ,\overrightarrow {AB} )} = 45^\circ \).
b) Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và vectơ \(\overrightarrow {AD} \):
Tương tự như câu a ta có: \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} \).
Mà góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {AD} \) là \(\widehat {DAC}\) và vì ABCD là hình vuông nên \(\widehat {DAC} = 45^\circ \).
Suy ra \(\widehat {(\overrightarrow {A'C'}, \overrightarrow {AD} )} = 45^\circ \).
c) Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và vectơ \(\overrightarrow {{B^\prime }B} \):
Gọi O và O’ lần lượt là tâm của hình vuông ABCD và A’B’C’D’.
Vì O và O’ lần lượt là trung điểm của cạnh BD và B’D’ nên OO’ là đường trung bình của BB’D’D, suy ra \(\overrightarrow {B'B} = \overrightarrow {O'O} \).
Mà \(O'O \bot AC\) nên \(\widehat {(\overrightarrow {A'C'}, \overrightarrow {B'B} )} = 90^\circ \).
HĐ6
Trả lời câu hỏi Hoạt động 6 trang 62 SGK Toán 12 Cùng khám phá
Trong không gian, cho hai vectơ \(\vec a,\vec b\) khác \(\vec 0\). Từ một điểm \(O\) tuỳ ý trong không gian, vẽ các vectơ \(\overrightarrow {{a^\prime }} ,\overrightarrow {{b^\prime }} \) sao cho \(\overrightarrow {{a^\prime }} = \vec a\), \(\overrightarrow {{b^\prime }} = \vec b\). (P) là mặt phẳng chứa giá của hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \) (Hình 2.21).
a) Trong mặt phẳng \((P)\), hãy viết biểu thức tính \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \).
b) Hãy so sánh \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \) với \(|\vec a| \cdot |\vec b| \cdot \cos (\vec a,\vec b)\).
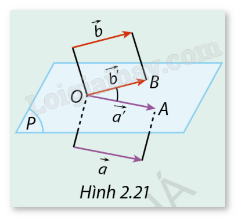
Phương pháp giải:
1. Sử dụng định nghĩa của tích vô hướng trong mặt phẳng \((P)\).
2. Sử dụng công thức của tích vô hướng để so sánh các biểu thức.
Lời giải chi tiết:
a) Trong mặt phẳng \((P)\), biểu thức tính \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \) được tính như sau:
\(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} = |\overrightarrow {{a^\prime }} | \cdot |\overrightarrow {{b^\prime }} | \cdot \cos \theta \)
trong đó \(\theta \) là góc giữa hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \).
b) Vì \(\overrightarrow {{a^\prime }} = \vec a\) và \(\overrightarrow {{b^\prime }} = \vec b\), nên:
\(|\overrightarrow {{a^\prime }} | = |\vec a|,|\overrightarrow {{b^\prime }} | = |\vec b|\)
Do đó, ta có:
\(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} = |\vec a| \cdot |\vec b| \cdot \cos \theta \)
trong đó \(\theta \) là góc giữa hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \).
Biểu thức này cho thấy rằng tích vô hướng của hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \) trong mặt phẳng \((P)\) là bằng tích của độ lớn của hai vectơ \(\vec a\) và \(\vec b\) với cosin của góc giữa chúng. Vì vậy:
\(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} = |\vec a| \cdot |\vec b| \cdot \cos (\vec a,\vec b)\)
Điều này chứng minh rằng tích vô hướng của \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \) trong mặt phẳng \((P)\) bằng tích vô hướng của \(\vec a\) và \(\vec b\).
LT7
Trả lời câu hỏi Luyện tập 7 trang 63 SGK Toán 12 Cùng khám phá
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy tính:
a) \(\overrightarrow {AB'} .\overrightarrow {A'C'} ;\)
b) \(\overrightarrow {AB'} .\overrightarrow {BD} ;\)
c) \(\overrightarrow {A'C'} .\overrightarrow {BB'} .\)
Phương pháp giải:
- Xác định độ dài của các vectơ và góc giữa chúng dựa vào tính chất của hình lập phương.
- Sử dụng công thức tích vô hướng \(\vec u \cdot \vec v = |\vec u||\vec v|\cos \theta \) để tính.
Lời giải chi tiết:
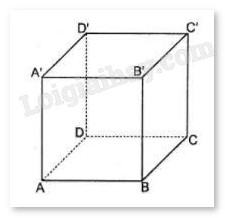
Gọi O và O’ lần lượt là tâm của hình vuông ABCD và A’B’C’D’.
a) Tính \(\overrightarrow {AB'} \cdot \overrightarrow {A'C'} \).
Độ dài của \(|\overrightarrow {AB'} | = |\overrightarrow {A'C'} | = a\sqrt 2 \) (vì AB' và A'C' là các cạnh đường chéo của các mặt bên của hình lập phương).
ABCD.A’B’C’D’ là hình lập phương nên \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} \).
Góc giữa \(\overrightarrow {AB'} \) và \(\overrightarrow {AC} \) là \({60^^\circ }\) vì chúng là hai cạnh của tam giác đều AB’C.
Do đó: \(\overrightarrow {AB'} .\overrightarrow {A'C'} = \left| {\overrightarrow {AB'} } \right|.\left| {\overrightarrow {A'C'} } \right|.\cos 60^\circ = a\sqrt 2 .a\sqrt 2 .\frac{1}{2} = {a^2}\).
b) Tính \(\overrightarrow {AB'} \cdot \overrightarrow {BD} \).
Độ dài của \(|\overrightarrow {AB'} | = a\sqrt 2 \) và \(|\overrightarrow {BD} | = a\sqrt 2 \) (cả hai đều là đường chéo của các mặt bên của hình lập phương).
Từ B vẽ một vectơ \(\overrightarrow {BE} \) bằng với vectơ \(\overrightarrow {AB'} \).
Vì D đối xứng với E qua tâm của hình vuông BB’C’C nên đường trung tuyến của tam giác cân BED có độ dài là \(\frac{{a\sqrt 2 }}{2}\).
Suy ra: \(\widehat {DBE} = 2\arccos \left( {\frac{{a\sqrt 2 }}{2}:a\sqrt 2 } \right) = 2\arccos \left( {\frac{1}{2}} \right) = 2.60^\circ = 120^\circ \).
Góc giữa \(\overrightarrow {AB'} \) và \(\overrightarrow {BD} \) cũng là góc giữa \(\overrightarrow {BE} \)và \(\overrightarrow {BD} \) là \(\widehat {DBE}\).
Do đó: \(\overrightarrow {AB'} .\overrightarrow {BD} = \left| {\overrightarrow {AB'} } \right|.\left| {\overrightarrow {BD} } \right|.\cos 120^\circ = a\sqrt 2 .a\sqrt 2 .\left( { - \frac{1}{2}} \right) = - {a^2}\).
c) Tính \(\overrightarrow {A'C'} \cdot \overrightarrow {BB'} \).
Độ dài của \(|\overrightarrow {A'C'} | = a\sqrt 2 \) và \(|\overrightarrow {BB'} | = a\).
ABCD.A’B’C’D’ là hình lập phương nên \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} ,\overrightarrow {BB'} = \overrightarrow {AA'} \).
Do \(\overrightarrow {AC} \) và \(\overrightarrow {AA'} \) vuông góc với nhau nên góc giữa \(\overrightarrow {A'C'} \) và \(\overrightarrow {BB'} \) Là 90°.
Suy ra: \(\overrightarrow {A'C'} .\overrightarrow {BB'} = \left| {\overrightarrow {A'C'} } \right|.\left| {\overrightarrow {BB'} } \right|.\cos 90^\circ = a\sqrt 2 .a.0 = 0\).
LT8
Trả lời câu hỏi Luyện tập 8 trang 63 SGK Toán 12 Cùng khám phá
Cho tứ diện ABCD có \(DA = DB = a\), \(BC = \frac{a}{2}\), \(AB \bot BC\) và \(\widehat {CBD} = {45^^\circ }\). Tính góc giữa hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
Phương pháp giải:
- Tính tích vô hướng của \(\overrightarrow {BC} .\overrightarrow {BD} \), từ đó suy ra mối liên hệ với tích vô hướng của hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
- Sử dụng công thức tích vô hướng giữa hai vectơ để tính cosin của góc giữa chúng:
\(\cos \theta = \frac{{\overrightarrow {AD} \cdot \overrightarrow {BC} }}{{|\overrightarrow {AD} | \times |\overrightarrow {BC} |}}\).
Lời giải chi tiết:
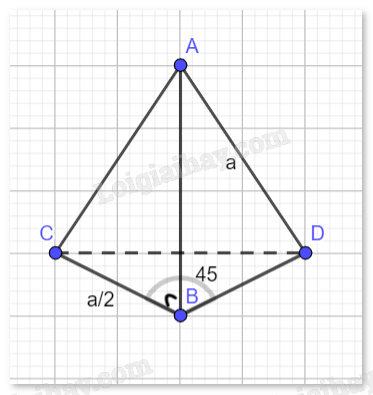
Ta có: \(\overrightarrow {BC} .\overrightarrow {BD} = BC.DB.\cos 45^\circ = \frac{a}{2}.a.\frac{{\sqrt 2 }}{2} = \frac{{{a^2}\sqrt 2 }}{4}\).
Mà: \(\overrightarrow {BC} .\overrightarrow {AD} = \overrightarrow {BC} .\overrightarrow {BD} + \overrightarrow {BC} .\overrightarrow {AB} \).
Suy ra: \(\overrightarrow {BC} .\overrightarrow {AD} = \frac{{{a^2}\sqrt 2 }}{4} + 0 = \frac{{{a^2}\sqrt 2 }}{4}\)(vì \(AB \bot BC\) nên \(\overrightarrow {BC} .\overrightarrow {AB} = 0\)).
Sử dụng công thức tích vô hướng giữa hai vectơ để tính cosin của góc giữa chúng:
\(\cos \theta = \frac{{\overrightarrow {AD} \cdot \overrightarrow {BC} }}{{|\overrightarrow {AD} | \times |\overrightarrow {BC} |}} = \frac{{\frac{{{a^2}\sqrt 2 }}{4}}}{{a.\frac{a}{2}}} = \frac{{\sqrt 2 }}{2}\).
Vậy góc giữa hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) là \(\arccos \left( {\frac{{\sqrt 2 }}{2}} \right) = 45^\circ \).
LT9
Trả lời câu hỏi Luyện tập 9 trang 64 SGK Toán 12 Cùng khám phá
Một chất điểm ở vị trí đỉnh \(A\) của hình lập phương ABCD.A'B'C'D'. Chất điểm chịu tác động bởi ba lực \(\vec a\), \(\vec b\), \(\vec c\) lần lượt cùng hướng với \(\overrightarrow {AD} \), \(\overrightarrow {AB} \) và \(\overrightarrow {AC'} \) như Hình 2.25. Cường độ của các lực \(\vec a\), \(\vec b\) và \(\vec c\) tương ứng là \(10{\rm{ N}}\), \(10{\rm{ N}}\) và \(20{\rm{ N}}\). Tính cường độ hợp lực của \(\vec a\), \(\vec b\) và \(\vec c\) (làm tròn kết quả đến hàng phần mười).
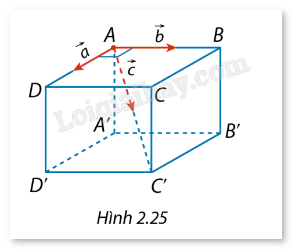
Phương pháp giải:
- Sử dụng công thức quy tắc hình bình hành để tính tổng hợp lực của \(\vec a\), \(\vec b\).
\(F{}^\text{2}=\text{}{{F}_{1}}{}^\text{2}+{{F}_{2}}{}^\text{2}+2.{{}_{1}}.{{F}_{2}}.\cos \alpha \).
- Sau đó sử dụng kết quả vừa tính để tính tổng hợp lực với \(\vec c\).
Lời giải chi tiết:
Vì ABCD.A’B’C’D’ là hình lập phương nên góc giữa \(\overrightarrow {AD} \)và \(\overrightarrow {AB} \) là 90°.
Suy ra lực \(\vec a\) vuông góc với \(\vec b\). Vậy hợp lực của hai lực \(\vec a\) và \(\vec b\) là:
\(\overrightarrow {{F_{ab}}} = \overrightarrow {{F_a}} + \overrightarrow {{F_b}} \Rightarrow {F_{ab}} = \sqrt {{F_a}^2 + {F_b}^2} = \sqrt {{{10}^2} + {{10}^2}} = 10\sqrt 2 N\).
Vì tam giác ACC’ là tam giác vuông tại C nên ta có:
\(AC' = \sqrt {A{C^2} + CC{'^2}} = \sqrt {A{C^2} + \frac{{A{C^2}}}{2}} = AC\sqrt {\frac{3}{2}} \) (vì CC’ là cạnh bên của hình lập phương còn AC là đường chéo của mặt bên nên \(CC' = \frac{{AC}}{{\sqrt 2 }}\)).
\(\cos \widehat {CAC'} = \frac{{AC}}{{AC'}} = \frac{{AC}}{{AC\sqrt {\frac{3}{2}} }} = \frac{{\sqrt 6 }}{3}\).
Hợp lực của \(\vec a\), \(\vec b\) và \(\vec c\) là:
\(F = \sqrt {{F_{ab}}^2 + F_c^2 + 2.{F_{ab}}.{F_c}.\cos \widehat {CAC'}} = \sqrt {{{\left( {10\sqrt 2 } \right)}^2} + {{20}^2} + 2.10\sqrt 2 .20.\frac{{\sqrt 6 }}{3}} = 32,6N\).