Giải mục 3 trang 54, 55, 56, 57 SGK Toán 10 tập 2 - Chân trời sáng tạo — Không quảng cáo

HĐ Khám phá 5

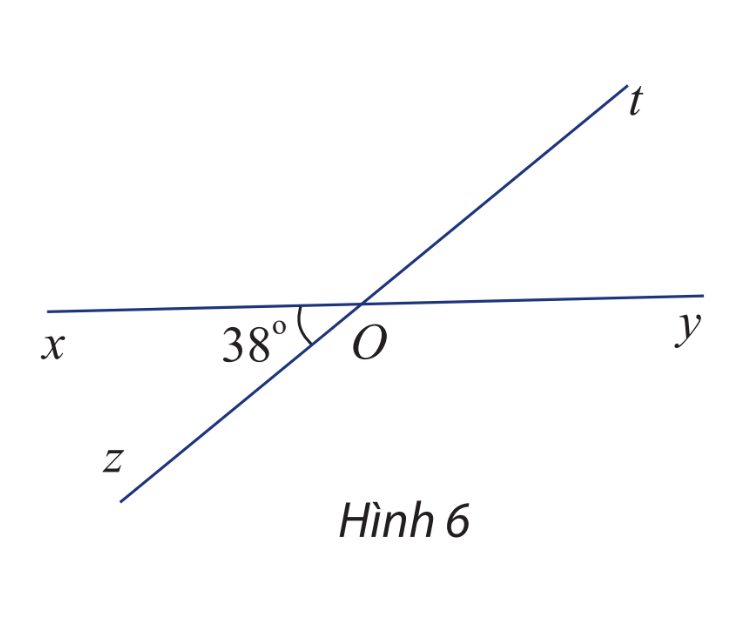
Cho hai đường thẳng xy và zt cắt nhau tại O và cho biết \(\widehat {xOz} = 38^\circ \) (hình 6)

Tính số đo các góc \(\widehat {xOt},\widehat {tOy}\) và \(\widehat {yOz}\)

Lời giải chi tiết:

Ta có hai góc \(\widehat {xOz}\) và \(\widehat {tOy}\) đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 38^\circ \)

hai góc \(\widehat {xOt}\) và \(\widehat {yOz}\) đối đỉnh nên \(\widehat {xOt} = \widehat {yOz}\)

\(\widehat {xOz}\) và \(\widehat {xOt}\) bù nhau nên \(\widehat {xOt} = 180^\circ  - \widehat {xOz} = 180^\circ  - 38^\circ  = 142^\circ \)

Vậy \(\widehat {xOz} = \widehat {tOy} = 38^\circ \) và \(\widehat {xOt} = \widehat {yOz} = 142^\circ \)

HĐ Khám phá 6

Cho hai đường thẳng

\({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\)  (\({a_1}^2 + {b_1}^2 > 0\)) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\)  \(\left( {{a_2}^2 + {b_2}^2 > 0} \right)\)

có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).

Tìm tọa độ \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \)và tính \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\)

Phương pháp giải:

+) Tọa độ của \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) được xác định từ pjuowng trình tổng quát của hai đường thẳng

+) Áp dụng biểu thức tọa độ của vectơ trong mặt phẳng

Lời giải chi tiết:

+) Từ phương trình \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_1}} \) là \(\left( {{a_1};{b_1}} \right)\)

+) Từ phương trình \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_2}} \) là \(\left( {{a_2};{b_2}} \right)\)

+) \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {{a_1}^2 + {b_1}^2} \sqrt {{a_2}^2 + {b_2}^2} }}\)

Thực hành 5

Tìm số đo của góc giữa hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\) trong các trường hợp sau

a) \({\Delta _1}:x + 3y - 7 = 0\) và \({\Delta _2}:x - 2y + 3 = 0\)

b)  \({\Delta _1}:4x - 2y + 5 = 0\) và \({\Delta _2}:\left\{ \begin{array}{l}x = t\\y = 13 + 2t\end{array} \right.\)

c) \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + t\\y = 3 + 2t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x =  - 7 + 2t\\y = 1 - t\end{array} \right.\)

Phương pháp giải:

Bước 1: Xác định vectơ pháp tuyến của hai đường thẳng đã cho

Bước 2: Tính số đo góc giữa hai đường thẳng bằng công thức \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {{a_1}^2 + {b_1}^2} \sqrt {{a_2}^2 + {b_2}^2} }}\)

Lời giải chi tiết:

a) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}}  = \left( {1;3} \right),\overrightarrow {{n_2}}  = \left( {1; - 2} \right)\)

Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {1.1 + 3.( - 2)} \right|}}{{\sqrt {{1^2} + {3^2}} \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} }} \approx 0,93 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) \approx 22^\circ 8'\)

b) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}}  = \left( {4; - 2} \right),\overrightarrow {{n_2}}  = \left( {2; - 1} \right)\)

Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {4.2 + ( - 2).( - 1)} \right|}}{{\sqrt {{4^2} + {{\left( { - 2} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = 1 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) = 0^\circ \)

c) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}}  = \left( {2; - 1} \right),\overrightarrow {{n_2}}  = \left( {1;2} \right)\)

Ta có \({a_1}{a_2} + {b_1}{b_2} = 2.1 + ( - 1).2 = 0\)

Suy ra \(\left( {{\Delta _1},{\Delta _2}} \right) = 90^\circ \)

Vận dụng 5

Tìm số đo của góc giữa hai đường thẳng là đồ thị của hai hàm số \(y = x\) và \(y = 2x + 1\)

Phương pháp giải:

Bước 1: Viết phương trình tổng quat từ đồ thị của hai hàm số đã cho

Bước 2: Xác định vectơ pháp tuyền

Bước 3: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {{a_1}^2 + {b_1}^2} \sqrt {{a_2}^2 + {b_2}^2} }}\)

Lời giải chi tiết:

Từ đồ thị hàm số ta có phương trình tổng quát

\(y = x \Leftrightarrow {d_1}:x - y = 0\), \(y = 2x + 1 \Leftrightarrow 2x - y + 1 = 0\)

Từ đó ta có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}}  = \left( {1; - 1} \right),\overrightarrow {{n_2}}  = \left( {2; - 1} \right)\)

\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {1.2 + ( - 1).( - 1)} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{3\sqrt {10} }}{{10}} \Rightarrow \left( {{d_1},{d_2}} \right) \approx 18^\circ 26'\)

Vậy góc giữa hai đường thẳng có đồ thị đã cho gần bằng \(18^\circ 26'\)