Giải mục 3 trang 63, 64 SGK Toán 10 tập 1 - Chân trời sáng tạo — Không quảng cáo

Thực hành 3

Tính:

$A = \sin {150^o} + \tan {135^o} + \cot {45^o}$

$B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}$

Phương pháp giải:

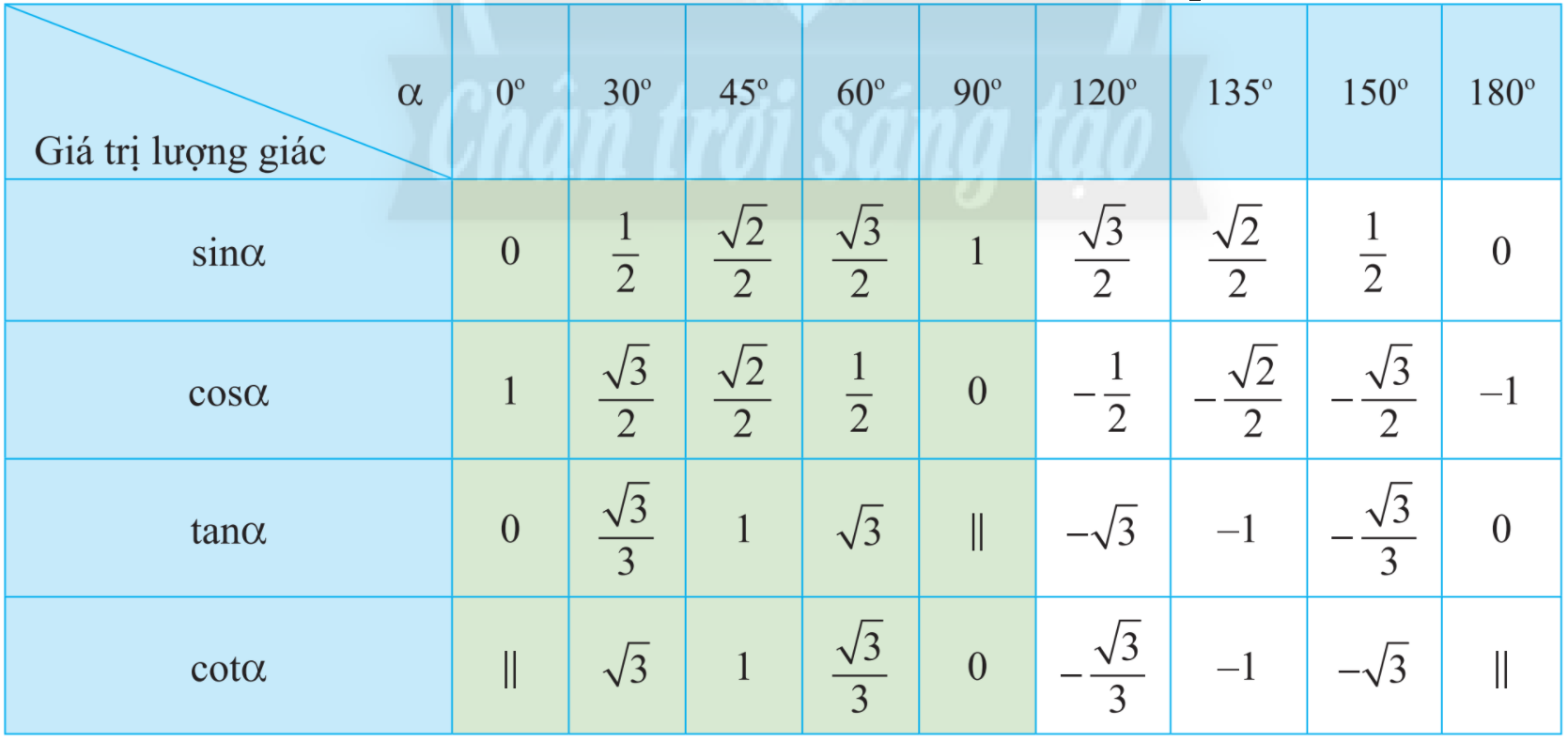
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt.

Lời giải chi tiết:

$A = \sin {150^o} + \tan {135^o} + \cot {45^o}$

Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:

$\sin {150^o} = \frac{1}{2};\tan {135^o} =  - 1;\cot {45^o} = 1.$

$\Rightarrow A = \frac{1}{2} - 1 + 1 = \frac{1}{2}.$

$B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}$

Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:

$\cos {30^o} = \frac{{\sqrt 3 }}{2};\tan {150^o} =  - \frac{{\sqrt 3 }}{3};\cot {135^o} =  - 1.$

$\Rightarrow B = 2.\frac{{\sqrt 3 }}{2} - 3.\left( { - \frac{{\sqrt 3 }}{3}} \right) + 1 = 2\sqrt 3  + 1.$

Vận dụng 2

Tìm góc $\alpha ({0^o} \le \alpha  \le {180^o})$ trong mỗi trường hợp sau:

a) $\sin \alpha  = \frac{{\sqrt 3 }}{2}$

b) $\cos \alpha  = \frac{{ - \sqrt 2 }}{2}$

c) $\tan \alpha  =  - 1$

d) $\cot \alpha  =  - \sqrt 3$

Phương pháp giải:

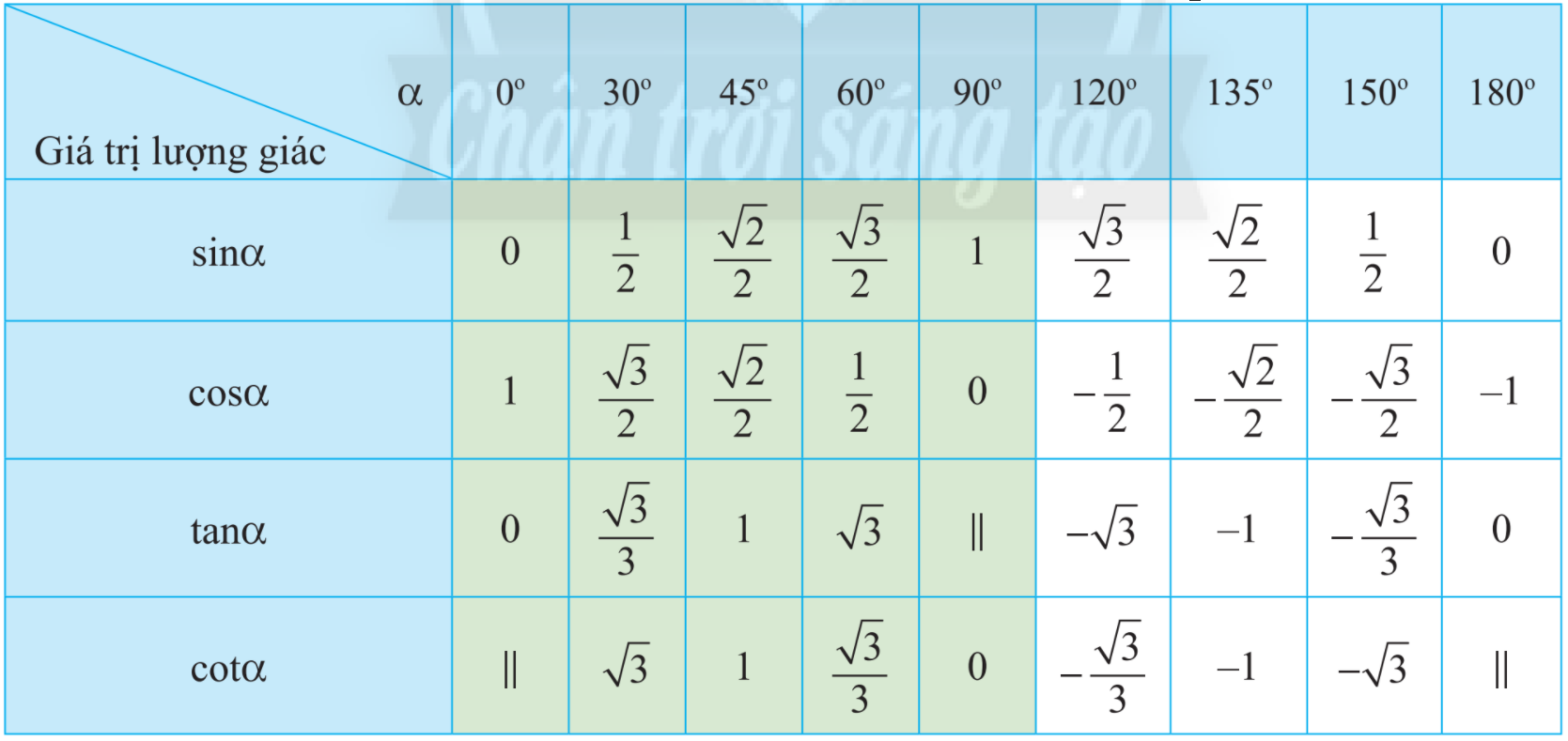
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt để tìm góc.

Lời giải chi tiết:

a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\sin \alpha$ ta có:

$\sin \alpha  = \frac{{\sqrt 3 }}{2}$ với $\alpha  = {60^o}$ và $\alpha  = {120^o}$

b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\cos \alpha$ ta có:

$\cos \alpha  = \frac{{ - \sqrt 2 }}{2}$ với $\alpha  = {135^o}$

c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\tan \alpha$ ta có:

$\tan \alpha  =  - 1$ với $\alpha  = {135^o}$

d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\cot \alpha$ ta có:

$\cot \alpha  =  - \sqrt 3$ với $\alpha  = {150^o}$