Giải mục 3 trang 70, 71, 72 SGK Toán 10 tập 1 - Chân trời sáng tạo — Không quảng cáo

HĐ Khám phá 3

Cho tam giác ABC như Hình 10.

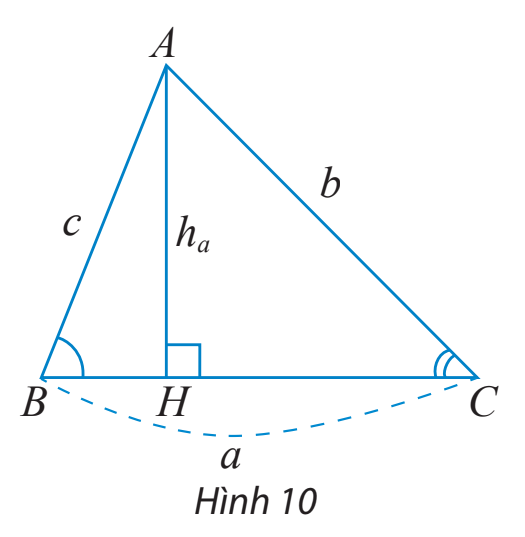
a) Viết công thức tính diện tích S của tam giác ABC theo a và ${h_a}$

b) Tính ${h_a}$ theo b và sinC.

c) Dùng hai kết quả trên để chứng minh công thức $S = \frac{1}{2}ab\sin C$

d) Dùng định lí sin và kết quả ở câu c) để chứng minh công thức $S = \frac{{abc}}{{4R}}$

Lời giải chi tiết:

a) Diện tích S của tam giác ABC là: $S = \frac{1}{2}a.{h_a}$

b) Xét tam giác vuông AHC ta có:  $\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b}$

$\Rightarrow {h_a} = b.\sin C$

c) Thay ${h_a} = b.\sin C$ vào công thức diện tích, ta được: $S = \frac{1}{2}ab\sin C$

d) Theo định lí sin ta có: $\frac{c}{{\sin C}} = 2R \Rightarrow \sin C = \frac{c}{{2R}}$

Thay vào công thức ở c) ta được: $S = \frac{1}{2}ab\frac{c}{{2R}} = \frac{{abc}}{{4R}}.$

HĐ Khám phá 4

Cho tam giác ABC có BC = a, AC = b, AB = c và (I;r) là đường tròn nội tiếp tam giác (Hình 11).

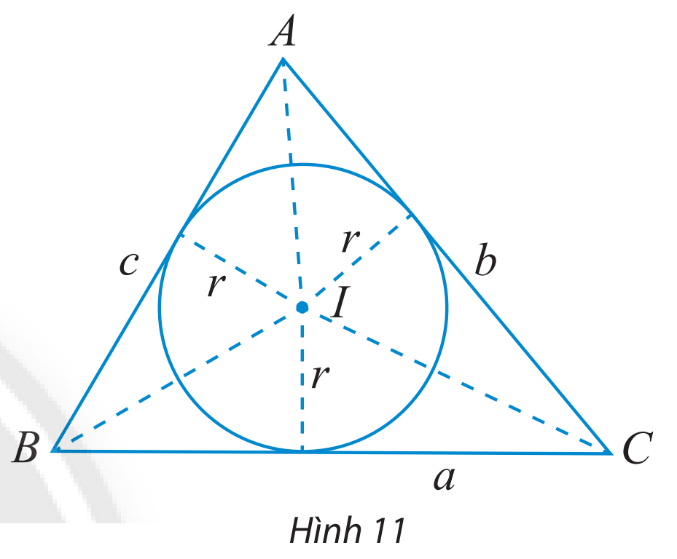
a) Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.

b) Dùng kết quả trên để chứng minh công thức tính diện tích tam giác ABC: $S = \frac{{r(a + b + c)}}{2}$

Lời giải chi tiết:

a) Diện tích ${S_1}$ của tam giác IAB là: ${S_1} = \frac{1}{2}r.AB = \frac{1}{2}r.c$

Diện tích ${S_2}$ của tam giác IAC là: ${S_2} = \frac{1}{2}r.AC = \frac{1}{2}r.b$

Diện tích ${S_3}$ của tam giác IBC là: ${S_3} = \frac{1}{2}r.BC = \frac{1}{2}r.a$

b) Diện tích S của tam giác ABC là:

$\begin{array}{l}S = {S_1} + {S_2} + {S_3} = \frac{1}{2}r.c + \frac{1}{2}r.b + \frac{1}{2}r.a = \frac{1}{2}r.(c + b + a)\\ \Leftrightarrow S = \frac{{r(a + b + c)}}{2}\end{array}$

Thực hành 3

Tính diện tích tam giác ABC và bán kính đường tròn ngoại tiếp tam giác ABC trong các trường hợp sau:

a) Các cạnh $b = 14,c = 35$ và $\widehat A = {60^o}$

b) Các cạnh $a = 4,b = 5,c = 3$

Phương pháp giải:

a) Áp dụng công thức: $S = \frac{1}{2}bc\sin A$

b) Áp dụng công thức Heron $S = \sqrt {p(p - a)(p - b)(p - c)}$

Lời giải chi tiết:

a) Áp dụng công thức: $S = \frac{1}{2}bc\sin A$, ta có:

$S = \frac{1}{2}.14.35.\sin {60^o} = \frac{1}{2}.14.35.\frac{{\sqrt 3 }}{2} \approx 212,2$

Áp dụng đl cosin, ta có: ${a^2} = {b^2} + {c^2} - 2bc.\cos A$

$\begin{array}{l} \Rightarrow {a^2} = {14^2} + {35^2} - 2.14.35.\cos {60^o} = 931\\ \Rightarrow a \approx 30,5 \end{array}$

$\Rightarrow R = \frac{a}{{2\sin A}} = \frac{{30,5}}{{2\sin {{60}^o}}} \approx 17,6$

b) Ta có: $p = \frac{1}{2}.(4 + 5 + 3) = 6$

Áp dụng công thức Heron, ta có:

$S = \sqrt {p(p - a)(p - b)(p - c)}  = \sqrt {6(6 - 4)(6 - 5)(6 - 3)}  = 6.$

Lại có: $S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{4.5.3}}{{4.6}} = 2,5.$

Vận dụng 3

Tính diện tích một cánh buồm hình tam giác. Biết cách buồm đó có chiều dài một cạnh là 3,2 m và hai góc kề cách đó có số đo là ${48^o}$ và ${105^o}$ (Hình 12).

Phương pháp giải:

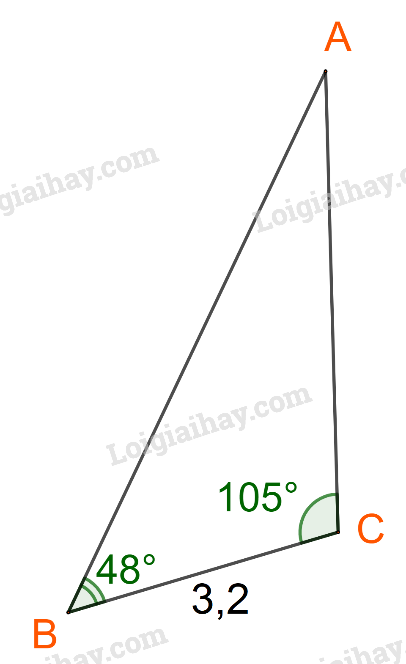
Bước 1: Áp dụng định lí sin tính AC.

Bước 2: Tính diện tích tam giác ABC bằng công thức $S = \frac{1}{2}ab\sin C$

Lời giải chi tiết:

Kí hiệu các điểm A, B, C như hình dưới

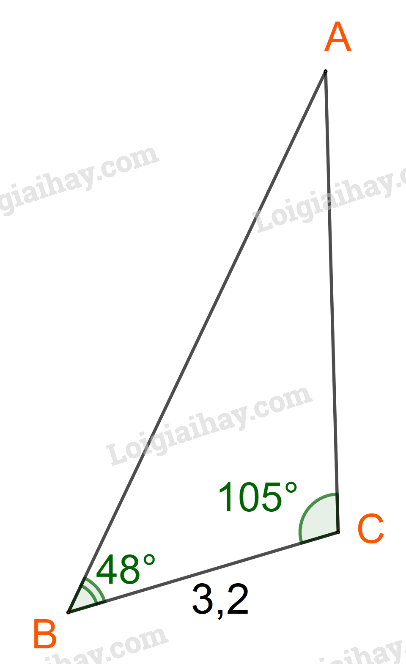
Đặt $AB = c,AC = b,BC = a.$

Ta có: $BC = 3,2;\widehat A = {180^o} - ({48^o} + {105^o}) = {27^o}$

Áp dụng định lí sin, ta có:

$\frac{b}{{\sin B}} = \frac{a}{{\sin A}} \Rightarrow AC = b = \frac{{a.\sin B}}{{\sin A}} = \frac{{3,2.\sin {{48}^o}}}{{\sin {{27}^o}}} \approx 5,24(m)$

Áp dụng công thức $S = \frac{1}{2}ab\sin C$ ta có:

$S = \frac{1}{2}.3,2.5,24\sin {105^o} \approx 8,1({m^2})$