Giải mục 3 trang 70, 71 SGK Toán 8 – Chân trời sáng tạo — Không quảng cáo

HĐ 3

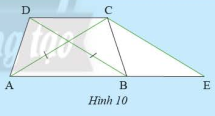
Cho hình thang \(ABCD\) có hai đáy là \(AB\) , \(CD\) và có hai đường chéo bằng nhau (Hình 10). Vẽ đường thẳng đi qua \(C\) , song song với \(BD\) và cắt \(AB\) tại \(E\) .

a) Tam giác \(CAE\) là tam giác gì? Vì sao?

b) So sánh tam giác \(ABD\) và tam giác \(BAC\)

Phương pháp giải:

Sử dụng tính chất của hình thang cân chứng minh \(\Delta CAE\) cân; \(\Delta ABD = \Delta BAC\)

Lời giải chi tiết:

a) Vì \(ABCD\) là hình thang cân (gt)

\( \Rightarrow AC = BD\) và \(AB\;{\rm{//}}\;CD\)

Xét \(\Delta BCD\) và \(\Delta CBE\) ta có:

\(\widehat {DCB} = \widehat {CBE}\) (do \(AB\) // \(CD\) )

\(BC\) chung

\(\widehat {CBD} = \widehat {BCE}\) (do \(CE\) // \(BD\) )

Suy ra \(\Delta BCD = \Delta CBE\) (g-c-g)

Suy ra \(BD = CE\) (hai cạnh tương ứng)

Mà \(AC = BD\) (cmt)

Suy ra \(AC = EC\)

Suy ra \(\Delta CAE\) cân tại \(C\)

b) Xét \(\Delta ABD\) và \(\Delta BAC\) ta có:

\(DA = BC\) (do \(ABCD\) là hình thang cân)

\(\widehat {DAB} = \widehat {CBA}\) (Do \(ABCD\) là hình thang cân)

\(AB\) chung

Suy ra \(\Delta ABD = \Delta BAC\) (c-g-c)

TH 3

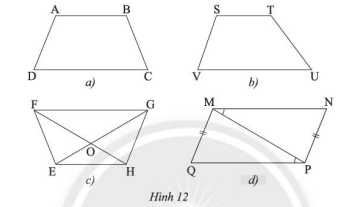
Sử dụng thước đo góc và thước đo độ dài để tìm hình thang cân trong các tứ giác ở Hình 12.

Phương pháp giải:

Sử dụng thước đo góc và đo độ dài và dấu hiệu nhận biết để tìm hình thang cân

Lời giải chi tiết:

Sau khi đo độ dài các cạnh và các góc, ta thấy \(ABCD\) , \(EFGH\) là các hình thang cân.

VD 4

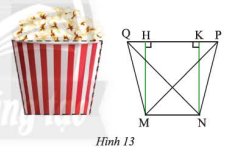
Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân \(MNPQ\) (Hình 13) với hai đáy \(MN = 6cm\) , \(PQ = 10\) cm và độ dài hai đường chéo \(MN = NQ = 8\sqrt 2 \) cm. Tính độ dài đường chéo và cạnh bên của hình thang

Phương pháp giải:

Chứng minh \(QH = KP\)

Tính độ dài các đoạn thẳng \(HK\) , \(QH\) , \(KP\)

Áp dụng định lý Pythagore tính độ dài \(MH\) , \(MQ\)

Lời giải chi tiết:

a) Xét \(\Delta MHQ\) và \(\Delta NKP\) ta có:

\(\widehat {MHQ} = \widehat {NKP} = 90^\circ \)

\(MQ = NP\) (do \(MNPQ\) là hình thang cân)

\(\widehat {MQP} = \widehat {NPQ}\) (do \(MNPQ\) là hình thang cân)

Suy ra: \(\Delta MHQ = \Delta NKP\) (ch – gn)

Suy ra: \(HQ = KP\) (hai cạnh tương ứng)

Suy ra \(HQ = KP = \frac{{PQ - HK}}{2} = \frac{{10 - 6}}{2} = 2\) (cm)

\(HP = 8\) cm

Áp dụng định lý Pythagore vào tam giác vuông \(MHP\) ta có:

\(M{H^2} = M{P^2} - H{P^2} = {\left( {8\sqrt 2 } \right)^2} - {8^2} = 128 - 64 = 64\)

\(MH = 8\) (cm)

Áp dụng định lý Pythagore vào tam giác vuông \(MHQ\) ta có:

\(M{Q^2} = M{H^2} + Q{H^2} = {8^2} + {2^2} = 68\)

\(MQ = \sqrt {68} \) (cm)