Giải mục 3 trang 72, 73, 74 SGK Toán 12 tập 2 - Chân trời sáng tạo
Ban Việt chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ Bảy và Chủ Nhật. Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào ngày thứ Bảy là 0,7. Hãy tìm các giá trị thích hợp thay vào ? ở sơ đồ hình cây sau:
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 72 SGK Toán 12 Chân trời sáng tạo
Ban Việt chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ Bảy và Chủ Nhật. Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào ngày thứ Bảy là 0,7.
Hãy tìm các giá trị thích hợp thay vào ? ở sơ đồ hình cây sau:
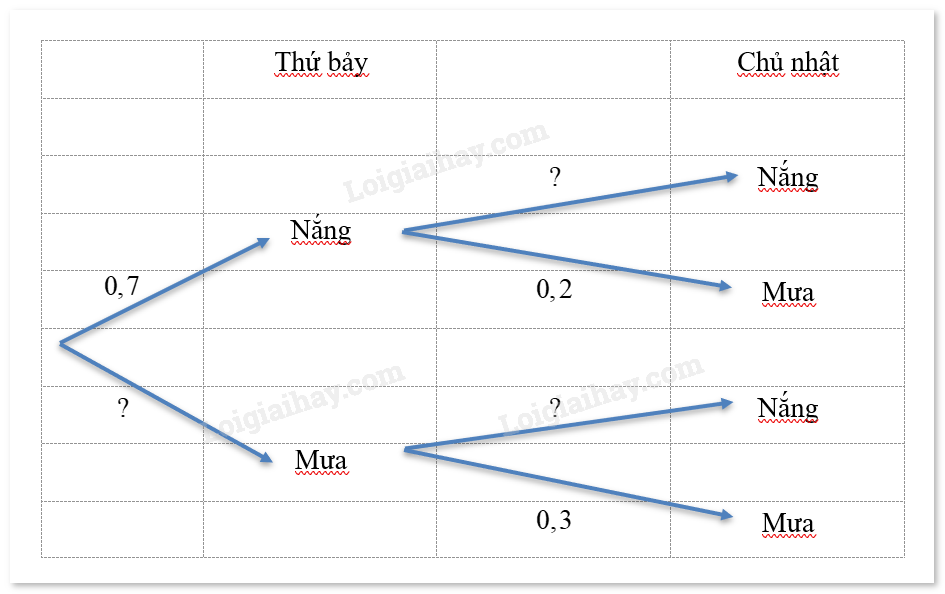
Phương pháp giải:
Do trong một ngày chỉ có thể xảy ra biến cố “Trời nắng” hoặc “Trời mưa”, nên sử dụng công thức cộng xác suất với các biến cố đối để điền các số vào dấu hỏi chấm.
Lời giải chi tiết:
Với ngày thứ 7, xác suất trời nắng là \(0,7\) nên xác suất trời mưa là \(1 - 0,7 = 0,3\).
Với ngày Chủ nhật:
- Trong trường hợp ngày thứ 7 trời nắng, xác suất trời mưa trong ngày Chủ nhật là \(0,2\). Suy ra xác suất trời nắng trong ngày Chủ nhật là \(1 - 0,2 = 0,8\).
- Trong trường hợp ngày thứ 7 trời mưa, xác suất trời mưa trong ngày Chủ nhật là \(0,3\). Suy ra xác suất trời nắng trong ngày Chủ nhật là \(1 - 0,3 = 0,7\).
Ta có sơ đồ sau:
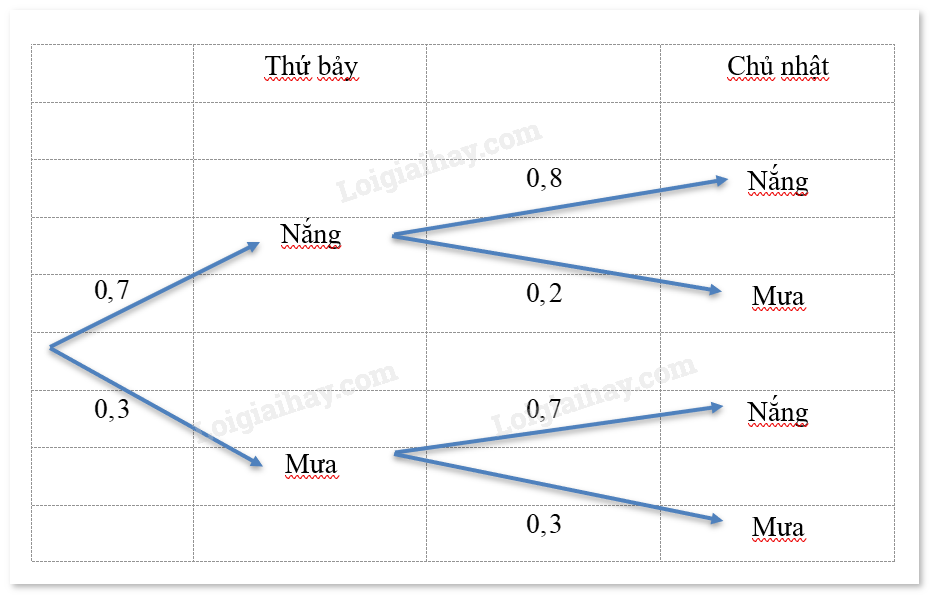
TH4
Trả lời câu hỏi Thực hành 4 trang 74 SGK Toán 12 Chân trời sáng tạo
Hộp thứ nhất có 4 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 5 viên bi xanh và 4 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên 1 viên bi từ hộp thứ hai. Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
\(A\): “Viên bi lấy ra từ hộp thứ nhất có màu xanh và viên bi lấy ra từ hộp thứ hai có màu đỏ”.
\(B\): “Hai viên bi lấy ra có cùng màu”.
Phương pháp giải:
Gọi \(M\) là biến cố “Viên bi lấy ra ở hộp thứ nhất có màu xanh” và \(N\) là biến cố “Viên bi lấy ra ở hộp thứ hai có màu đỏ”. Sử dụng sơ đồ hình cây, từ đó tính được \(P\left( A \right)\) và \(P\left( B \right)\).
Lời giải chi tiết:
Gọi \(M\) là biến cố “Viên bi lấy ra ở hộp thứ nhất có màu xanh” và \(N\) là biến cố “Viên bi lấy ra ở hộp thứ hai có màu đỏ”.
Xác suất để lấy ra được 1 viên bi xanh ở hộp thứ nhất là \(\frac{4}{{10}} = 0,4\).
Nếu ta lấy được viên bi xanh ở hộp thứ nhất và bỏ vào hộp thứ hai thì hộp thứ hai có 6 viên bi xanh và 4 viên bi đỏ. Suy ra xác suất để lấy ra được 1 viên bi đỏ là \(\frac{4}{{10}} = 0,4\).
Nếu ta lấy được viên bi đỏ ở hộp thứ nhất và bỏ vào hộp thứ hai thì hộp thứ hai có 5 viên bi xanh và 5 viên bi đỏ. Suy ra xác suất để lấy được 1 viên bi đỏ là \(\frac{5}{{10}} = 0,5\).
Ta có sơ đồ hình cây sau:
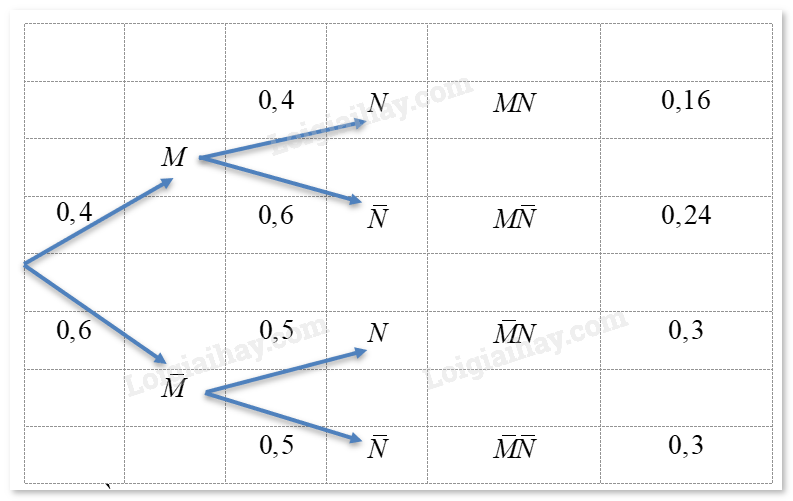
Dựa vào sơ đồ hình cây, ta có:
\(P\left( A \right) = P\left( {MN} \right) = 0,16.\)
\(P\left( B \right) = P\left( {M\bar N} \right) + P\left( {\bar MN} \right) = 0,24 + 0,3 = 0,54.\)
VD3
Trả lời câu hỏi Vận dụng 3 trang 74 SGK Toán 12 Chân trời sáng tạo
Một trường đại học tiến hành khảo sát tình trạng việc làm sau khi tốt nghiệp của sinh viên. Kết quả khảo sát cho thấy tỉ lệ người tìm được việc làm đúng chuyên ngành là 85% đối với sinh viên loại giỏi và 70% đối với sinh viên tốt nghiệp loại khác.
Tỉ lệ sinh viên tốt nghiệp loại giỏi là 30%. Gặp ngẫu nhiên một sinh viên đã tốt nghiệp của trường.
Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
\(C\): “Sinh viên tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành”.
\(D\): “Sinh viên không tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành”.
Phương pháp giải:
Gọi \(M\) là biến cố “Sinh viên tốt nghiệp loại giỏi” và \(N\) là biến cố “Sinh viên tìm được việc làm đúng chuyên ngành”. Sử dụng sơ đồ hình cây, từ đó tính được \(P\left( C \right)\) và \(P\left( D \right)\).
Lời giải chi tiết:
Gọi \(M\) là biến cố “Sinh viên tốt nghiệp loại giỏi” và \(N\) là biến cố “Sinh viên tìm được việc làm đúng chuyên ngành”.
Theo đề bài, ta có sơ đồ hình cây sau:

Từ sơ đồ hình cây, ta suy ra \(P\left( C \right) = P\left( {MN} \right) = 0,255\) và \(P\left( D \right) = P\left( {\bar MN} \right) = 0,49.\)