Giải mục 4 trang 38, 39, 40 SGK Toán 12 tập 2 - Chân trời sáng tạo
Cho hai mặt phẳng \(\left( \alpha \right)\), \(\left( \beta \right)\) có phương trình là \(\left( \alpha \right):x - 2y + 3z + 1 = 0\) và \(\left( \beta \right):2x - 4y + 6z + 1 = 0\). a) Nêu nhận xét về các vectơ pháp tuyến của hai mặt phẳng trên. b) Cho điểm \(M\left( { - 1;0;0} \right)\). Hãy cho biết các mặt phẳng \(\left( \alpha \right)\), \(\left( \beta \right)\) có đi qua \(M\) không. c) Giải thích tại sao \(\left( \alpha \right)\) song song với \(\left( \beta \right)\).
HĐ7
Trả lời câu hỏi Hoạt động 7 trang 38 SGK Toán 12 Chân trời sáng tạo
Cho hai mặt phẳng \(\left( \alpha \right)\), \(\left( \beta \right)\) có phương trình là \(\left( \alpha \right):x - 2y + 3z + 1 = 0\) và \(\left( \beta \right):2x - 4y + 6z + 1 = 0\).
a) Nêu nhận xét về các vectơ pháp tuyến của hai mặt phẳng trên.
b) Cho điểm \(M\left( { - 1;0;0} \right)\). Hãy cho biết các mặt phẳng \(\left( \alpha \right)\), \(\left( \beta \right)\) có đi qua \(M\) không.
c) Giải thích tại sao \(\left( \alpha \right)\) song song với \(\left( \beta \right)\).
Phương pháp giải:
a) Chỉ ra một vectơ pháp tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\), rồi nhận xét.
b) Thay toạ độ điểm \(M\) lần lượt vào phương trình các mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) rồi nhận xét.
c) Từ các kết quả ở câu a và b rồi giải thích.
Lời giải chi tiết:
a) Một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) là \(\overrightarrow {{n_{\left( \alpha \right)}}} = \left( {1; - 2;3} \right)\).
Một vectơ pháp tuyến của mặt phẳng \(\left( \beta \right)\) là \(\overrightarrow {{n_{\left( \beta \right)}}} = \left( {2; - 4;6} \right)\).
Do \(\frac{1}{2} = \frac{{ - 2}}{{ - 4}} = \frac{3}{6}\), nên \(\overrightarrow {{n_{\left( \alpha \right)}}} \) và \(\overrightarrow {{n_{\left( \beta \right)}}} \) cùng phương.
b) Thay toạ độ của điểm \(M\left( { - 1;0;0} \right)\) vào phương trình mặt phẳng \(\left( \alpha \right)\) ta có:
\( - 1 - 2.0 + 3.0 + 1 = 0\)
Như vậy mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(M\left( { - 1;0;0} \right)\).
Thay toạ độ của điểm \(M\left( { - 1;0;0} \right)\) vào phương trình mặt phẳng \(\left( \beta \right)\) ta có:
\(2\left( { - 1} \right) - 4.0 + 6.0 + 1 = - 1 \ne 0\)
Như vậy mặt phẳng \(\left( \beta \right)\) không đi qua điểm \(M\left( { - 1;0;0} \right)\).
c) Theo câu a, do \(\overrightarrow {{n_{\left( \alpha \right)}}} \) và \(\overrightarrow {{n_{\left( \beta \right)}}} \) cùng phương, nên giá của \(\overrightarrow {{n_{\left( \alpha \right)}}} \) và \(\overrightarrow {{n_{\left( \beta \right)}}} \) song song hoặc trùng nhau. Mặt khác, do \(\overrightarrow {{n_{\left( \alpha \right)}}} \) có giá vuông góc với \(\left( \alpha \right)\), \(\overrightarrow {{n_{\left( \beta \right)}}} \) có giá vuông góc với \(\left( \beta \right)\), ta suy ra hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song hoặc trùng nhau. Hơn nữa, theo câu b, điểm \(M\left( { - 1;0;0} \right)\) thuộc \(\left( \alpha \right)\) nhưng không thuộc \(\left( \beta \right)\), suy ra \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.
TH5
Trả lời câu hỏi Thực hành 5 trang 39 SGK Toán 12 Chân trời sáng tạo
Mặt phẳng \(\left( E \right):2x - y + 8z + 1 = 0\) song song với mặt phẳng nào sau đây?
a) \(\left( F \right):8x - 4y + 32z + 7 = 0\)
b) \(\left( H \right):6x - 3y + 24z + 3 = 0\)
c) \(\left( G \right):10x - 5y + 41z + 1 = 0\)
Phương pháp giải:
Xác định các vectơ pháp tuyến của các mặt phẳng \(\left( E \right)\), \(\left( F \right)\), \(\left( H \right)\), \(\left( G \right)\), rồi chỉ ra mặt phẳng song song với mặt phẳng \(\left( E \right)\).
Lời giải chi tiết:
Các mặt phẳng \(\left( E \right)\), \(\left( F \right)\), \(\left( H \right)\), \(\left( G \right)\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_{\left( E \right)}}} = \left( {2; - 1;8} \right)\), \(\overrightarrow {{n_{\left( F \right)}}} = \left( {8; - 4;32} \right)\), \(\overrightarrow {{n_{\left( H \right)}}} = \left( {6; - 3;24} \right)\), \(\overrightarrow {{n_{\left( G \right)}}} = \left( {10; - 5;41} \right)\).
Ta có \(\overrightarrow {{n_{\left( F \right)}}} = 4\overrightarrow {{n_{\left( E \right)}}} \), nhưng \(7 \ne 4.1\). Vậy \(\left( E \right)\parallel \left( F \right)\).
Ta có \(\overrightarrow {{n_{\left( H \right)}}} = 3\overrightarrow {{n_{\left( E \right)}}} \) và \(3 = 3.1\). Vậy \(\left( E \right) \equiv \left( H \right)\).
Ta có \(\frac{2}{{10}} = \frac{{ - 1}}{{ - 5}} \ne \frac{8}{{41}}\), suy ra \(\overrightarrow {{n_{\left( E \right)}}} \) và \(\overrightarrow {{n_{\left( G \right)}}} \) không cùng phương. Vậy \(\left( E \right)\) cắt \(\left( G \right)\).
VD4
Trả lời câu hỏi Vận dụng 4 trang 40 SGK Toán 12 Chân trời sáng tạo
Trên bản thiết kế đồ hoạ 3D của một cánh đồng điện mặt trời trong không gian \(Oxyz\), một tấm pin nằm trên mặt phẳng \(\left( P \right):6x + 5y + z + 2 = 0\); một tấm pin khác nằm trên mặt phẳng \(\left( Q \right)\) đi qua điểm \(M\left( {1;1;1} \right)\) và song song với \(\left( P \right)\). Viết phương trình mặt phẳng \(\left( Q \right)\).

Phương pháp giải:
Dễ dàng thấy được
\(M\left( {1;1;1} \right)\) không nằm trên \(\left( P \right)\). Do \(\left( P \right)\parallel \left( Q \right)\), nên \(\left( Q \right)\) nhận vectơ pháp tuyến của \(\left( P \right)\) làm vectơ pháp tuyến của mình. Từ đó viết phương trình mặt phẳng \(\left( Q \right)\).
Lời giải chi tiết:
Dễ dàng thấy được \(M\left( {1;1;1} \right)\) không nằm trên \(\left( P \right)\).
Do \(\left( P \right)\parallel \left( Q \right)\), nên một vectơ pháp tuyến của \(\left( Q \right)\) là \(\vec n = \left( {6;5;1} \right)\).
Phương trình mặt phẳng \(\left( Q \right)\) đi qua \(M\left( {1;1;1} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {6;5;1} \right)\) là \(6\left( {x - 1} \right) + 5\left( {y - 1} \right) + 1\left( {z - 1} \right) = 0 \Leftrightarrow 6x + 5y + z - 12 = 0\)
HĐ8
Trả lời câu hỏi Hoạt động 8 trang 40 SGK Toán 12 Chân trời sáng tạo
Cho hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có phương trình là \(\left( \alpha \right):3x + 2y + z + 1 = 0\) và \(\left( \beta \right):5x - 10y + 5z + 9 = 0\).
a) Chỉ ra hai vectơ \(\overrightarrow {{n_1}} \), \(\overrightarrow {{n_2}} \) lần lượt là vectơ pháp tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\).
b) Tính tích vô hướng \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} \) và nêu nhận xét về hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\).
Phương pháp giải:
a) Chỉ ra các vectơ pháp tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) dựa vào phương trình các mặt phẳng.
b) Sử dụng công thức tích vô hướng, tính tích \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} \) và rút ra kết luận về hai mặt phẳng.
Lời giải chi tiết:
a) Mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có các vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {3;2;1} \right)\) và \(\overrightarrow {{n_2}} = \left( {5; - 10;5} \right)\).
b) Ta có \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 3.5 + 2.\left( { - 10} \right) + 1.5 = 0\). Vậy hai vectơ \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) có giá vuông góc với nhau. Do \(\overrightarrow {{n_1}} \) có giá vuông góc với \(\left( \alpha \right)\), \(\overrightarrow {{n_2}} \) có giá vuông góc với \(\left( \beta \right)\) nên \(\left( \alpha \right)\) và \(\left( \beta \right)\) vuông góc với nhau.
TH6
Trả lời câu hỏi Thực hành 6 trang 40 SGK Toán 12 Chân trời sáng tạo
Tìm các cặp mặt phẳng vuông góc trong các mặt phẳng sau:
\(\left( F \right):3x + 2y + 5z + 3 = 0\)
\(\left( H \right):x - 4y + z + 23 = 0\)
\(\left( G \right):x - y + 3z + 24 = 0\)
Phương pháp giải:
Chỉ ra các vectơ pháp tuyến lần lượt của các mặt phẳng, sau đó tính tích vô hướng để chọn ra các cặp vectơ có tích vô hướng bằng 0.
Lời giải chi tiết:
Các mặt phẳng \(\left( F \right)\), \(\left( H \right)\), \(\left( G \right)\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_{\left( F \right)}}} = \left( {3;2;5} \right)\), \(\overrightarrow {{n_{\left( H \right)}}} = \left( {1; - 4;1} \right)\), \(\overrightarrow {{n_{\left( G \right)}}} = \left( {1; - 1;3} \right)\).
Ta có \(\overrightarrow {{n_{\left( F \right)}}} .\overrightarrow {{n_{\left( H \right)}}} = 3.1 + 2.\left( { - 4} \right) + 5.1 = 0\). Vậy \(\left( F \right) \bot \left( H \right)\).
VD5
Trả lời câu hỏi Vận dụng 5 trang 40 SGK Toán 12 Chân trời sáng tạo
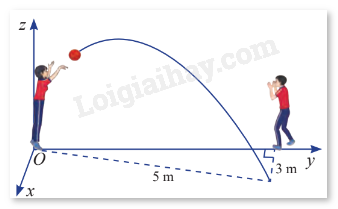
Hai học sinh đang chuyền bóng. Bạn nữ ném bóng cho bạn nam. Quả bóng bay trên không, lệch sang phải và rơi xuống tại vị trí cách bạn nam 3 m, cách bạn nữ 5 m. Cho biết quỹ đạo của quả bóng nằm trong mặt phẳng \(\left( P \right)\) vuông góc với mặt đất. Hãy viết phương trình của \(\left( P \right)\) trong không gian \(Oxyz\) được mô tả trong hình vẽ.
Phương pháp giải:
Do \(\left( P \right) \bot \left( {Oxy} \right)\), mà vectơ pháp tuyến \(\vec n\) của \(\left( {Oxy} \right)\) có giá vuông góc với \(\left( {Oxy} \right)\), nên giá của \(\vec n\) song song hoặc nằm trên \(\left( P \right)\). Như vậy \(\vec n\) là một vectơ chỉ phương của \(\left( P \right)\).
Mặt khác, theo hình vẽ, gọi \(A\) là điểm rơi của quả bóng trên mặt đất. Dễ dàng thấy được \({z_A} = 0\) và \({x_A} = 3\). Trên mặt phẳng \(\left( {Oxy} \right)\), sử dụng định lý Pythagore để xác định \({y_A}\) . Mặt phẳng \(\left( P \right)\) đi qua \(O\) và \(A\) nên \(\overrightarrow {OA} \) là một vectơ chỉ phương khác của \(\left( P \right)\). Dễ thấy rằng \(\overrightarrow {OA} \) và \(\vec n\) không cùng phương, từ đó tính tích có hướng của hai vectơ \(\overrightarrow {OA} \) và \(\vec n\) để tìm được một vectơ pháp tuyến của \(\left( P \right)\).
Lời giải chi tiết:
Mặt phẳng \(\left( {Oxy} \right)\) có một vectơ pháp tuyến là \(\vec n = \left( {0;0;1} \right)\).
Do \(\left( P \right) \bot \left( {Oxy} \right)\), mà vectơ pháp tuyến \(\vec n\) của \(\left( {Oxy} \right)\) có giá vuông góc với \(\left( {Oxy} \right)\), nên giá của \(\vec n\) song song hoặc nằm trên \(\left( P \right)\). Như vậy \(\vec n\) là một vectơ chỉ phương của \(\left( P \right)\).
Mặt khác, theo hình vẽ, gọi \(A\) là điểm rơi của quả bóng trên mặt đất. Dễ dàng thấy được \({z_A} = 0\) và \({x_A} = 3\). Trên mặt phẳng \(\left( {Oxy} \right)\), ta có \(OA = 5\) và \({y_A} > 0\). Như vậy tung độ của \(A\) là \({y_A} = \sqrt {{5^2} - {3^2}} = 4\). Vậy ta có \(A\left( {3;4;0} \right)\)
Theo hình vẽ,\(\left( P \right)\) đi qua điểm \(O\left( {0;0;0} \right)\) và \(A\left( {3;4;0} \right)\), nên \(\overrightarrow {OA} \left( {3;4;0} \right)\) là một vectơ chỉ phương khác của \(\left( P \right)\). Ta dễ thấy rằng \(\vec n = \left( {0;0;1} \right)\) và \(\overrightarrow {OA} \left( {3;4;0} \right)\) là hai vectơ không cùng phương, do đó \(\vec n\) và \(\overrightarrow {OA} \) là một cặp vectơ chỉ phương của \(\left( P \right)\).
Như vậy một vectơ pháp tuyến của \(\left( P \right)\) là:
\(\overrightarrow {{n_{\left( P \right)}}} = \left[ {\vec n,\overrightarrow {OA} } \right] = \left( {0.0 - 1.4;1.3 - 0.0;0.4 - 0.3} \right) = \left( { - 4;3;0} \right)\).
Vậy phương trình mặt phẳng \(\left( P \right)\) đi qua \(O\left( {0;0;0} \right)\) và có một vectơ pháp tuyến \(\overrightarrow {{n_{\left( P \right)}}} = \left( { - 4;3;0} \right)\) là \( - 4\left( {x - 0} \right) + 3\left( {y - 0} \right) + 0\left( {z - 0} \right) = 0 \Leftrightarrow - 4x + 3y = 0\)