Giải mục 4 trang 23, 24 SGK Toán 11 tập 2 - Kết nối tri thức
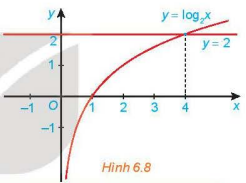
Cho đồ thị của hàm số (y = {log _2}x) và y = 2 như Hình 6.8.
HĐ4
Cho đồ thị của hàm số \(y = {\log _2}x\) và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {\log _2}x\) nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình \({\log _2}x > 2.\)
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
Khoảng giá trị của x mà đồ thị hàm số \(y = {\log _2}x\) nằm phía trên đường thẳng y = 2 là \(\left( {4; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \({\log _2}x > 2\) là \(\left( {4; + \infty } \right)\)
LT4
Giải các bất phương trình sau:
a) \({\log _{\frac{1}{7}}}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right);\)
b) \(2\log \left( {2x + 1} \right) > 3.\)
Phương pháp giải:
Xét bất phương trình dạng \({\log _a}x > b\)
+) a > 1, nghiệm của bất phương trình là \(x > {a^b}\)
+) 0 < a < 1, nghiệm của bất phương trình là \(0 < x < {a^b}\)
Lời giải chi tiết:
a) \({\log _{\frac{1}{7}}}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right)\) (ĐK: \(x + 1 > 0;2 - x > 0 \Leftrightarrow - 1 < x < 2\))
\(\begin{array}{l} \Leftrightarrow {\log _{{7^{ - 1}}}}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right)\\ \Leftrightarrow - {\log _7}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right)\\ \Leftrightarrow {\log _7}{\left( {x + 1} \right)^{ - 1}} > {\log _7}\left( {2 - x} \right)\\ \Leftrightarrow {\left( {x + 1} \right)^{ - 1}} > 2 - x\\ \Leftrightarrow \frac{1}{{x + 1}} - 2 + x > 0\\ \Leftrightarrow \frac{{1 + \left( {x - 2} \right)\left( {x + 1} \right)}}{{x + 1}} > 0\\ \Leftrightarrow \frac{{1 + {x^2} - x - 2}}{{x + 1}} > 0 \Leftrightarrow \frac{{{x^2} - x - 1}}{{x + 1}} > 0\end{array}\)
Mà – 1 < x < 2 nên x + 1 > 0
\( \Leftrightarrow {x^2} - x - 1 > 0 \Leftrightarrow \left[ \begin{array}{l}x < \frac{{1 - \sqrt 5 }}{2}\\x > \frac{{1 + \sqrt 5 }}{2}\end{array} \right.\)
KHĐK ta có \(\left[ \begin{array}{l} - 1 < x < \frac{{1 - \sqrt 5 }}{2}\\\frac{{1 + \sqrt 5 }}{2} < x < 2\end{array} \right.\)
b) \(2\log \left( {2x + 1} \right) > 3\) (ĐK: \(2x + 1 > 0 \Leftrightarrow x > \frac{{ - 1}}{2}\))
\(\begin{array}{l} \Leftrightarrow \log \left( {2x + 1} \right) > \frac{3}{2}\\ \Leftrightarrow 2x + 1 > {10^{\frac{3}{2}}} = 10\sqrt {10} \\ \Leftrightarrow x > \frac{{10\sqrt {10} - 1}}{2}\end{array}\)
KHĐK ta có \(x > \frac{{10\sqrt {10} - 1}}{2}\)
VD
Áp suất khí quyển p (tính bằng kilopascal, viết tắt là kPa) ở độ cao h (so với mực nước biển, tính bằng km) được tính theo công thức sau:
\(\ln \left( {\frac{p}{{100}}} \right) = - \frac{h}{7}.\)
(Theo britannica.com )
a) Tính áp suất khí quyển ở độ cao 4 km.
b) Ở độ cao trên 10 km thì áp suất khí quyển sẽ như thế nào?
Phương pháp giải:
Sử dụng công thức \(\ln \left( {\frac{p}{{100}}} \right) = - \frac{h}{7}.\)
Lời giải chi tiết:
a) Ở độ cao 4km ta có: \(\ln \left( {\frac{p}{{100}}} \right) = - \frac{4}{7} \Leftrightarrow \frac{p}{{100}} = {e^{\frac{{ - 4}}{7}}} \Leftrightarrow p = 56,4718122\)
Vậy áp suất khí quyển ở độ cao 4 km là 56,4718122 kPa.
b) Ở độ cao trên 10km ta có:
\(h > 10 \Leftrightarrow \ln \left( {\frac{p}{{100}}} \right) < - \frac{{10}}{7} \Leftrightarrow \frac{p}{{100}} < {e^{\frac{{ - 10}}{7}}} \Leftrightarrow p < 23,96510364\)
Vậy ở độ cao trên 10 km thì áp suất khí quyển bé hơn 29,96510364 kPa.