Giải mục I trang 73, 74 SGK Toán 10 tập 2 - Cánh diều — Không quảng cáo

HĐ Khởi động

Lời giải chi tiết:

Để xác định tọa độ của máy bay ta phải lập phương trình quỹ đạo bay của máy bay hay chính là lập phương trình đường thẳng.

Hoạt động 1

Trong mặt phẳng toạ độ Oxy, cho đường thẳng $\Delta$ . Vẽ vectơ $\overrightarrow u$ ($\overrightarrow u  \ne \overrightarrow 0$) có giá song song (hoặc trùng) với đường thẳng $\Delta$.

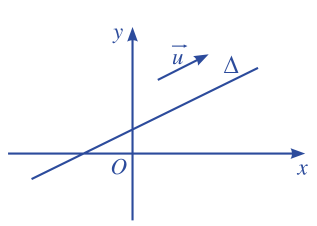
Lời giải chi tiết:

Nhận xét

• Nếu ủ là một vectơ chỉ phương của A thì $k\overrightarrow u$ ($k \ne 0$)cũng là một vectơ chỉ phương của A.

• Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vectơ chỉ phương của đường thẳng đó.

Hoạt động 2

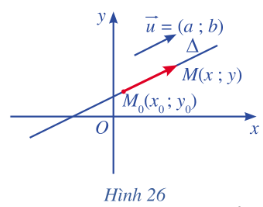
Trong mặt phẳng toạ độ Oxy, cho đường thẳng $\Delta$ đi qua điểm ${M_o}\left( {{x_o};{y_o}} \right)$ và có vectơ chỉ phương$\overrightarrow u {\rm{ }} = \left( {a;{\rm{ }}b} \right)$ . Xét điểm M(x ; y) nằm trên $\Delta$ (Hình 26).

a) Nhận xét về phương của hai vectơ $\overrightarrow u {\rm{ }}$và$\overrightarrow {{M_o}M}$ .

b) Chứng minh có số thực t sao cho $\overrightarrow {{M_o}M}$ = $t\overrightarrow u {\rm{ }}$.

c) Biểu diễn toạ độ của điểm M qua toạ độ của điểm ${M_o}$ và toạ độ của vectơ chỉ phương $\overrightarrow u {\rm{ }}$.

Lời giải chi tiết:

a) Hai vectơ $\overrightarrow u {\rm{ }}$và $\overrightarrow {{M_o}M}$cùng phương với nhau.

b) Xét $M\left( {x;y} \right)$. Vì cùng phương với  nên có số thực t sao cho $\overrightarrow {{M_o}M}  = t\overrightarrow u {\rm{ }}$

c) Do $\overrightarrow {{M_o}M}  = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow u  = \left( {a;b} \right)$ nên:

$\overrightarrow {{M_o}M}  = t\overrightarrow u {\rm{ }} \Leftrightarrow \left\{ \begin{array}{l}x - {x_o} = at\\y - {y_o} = bt\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = {x_o} + at\\y = {y_o} + bt\end{array} \right.$

Vậy tọa độ điểm M là: $M\left( {{x_o} + at;{y_o} + bt} \right)$

Luyện tập – vận dụng 1

Cho đường thẳng $\Delta$có phương trình tham số $\left\{ \begin{array}{l}x = 1 - 2t\\y =  - 2 + t\end{array} \right.$

a) Chỉ ra tọa độ của hai điểm thuộc đường thẳng $\Delta$.

b) Điểm nào trong các điểm $C( - 1: - 1).{\rm{ }}D\left( {1:3} \right)$ thuộc đường thẳng $\Delta$?

Lời giải chi tiết:

a) Chọn $t = 0;t = 1$ ta lần được được 2 điểm A và B thuộc đường thẳng $\Delta$ là: $A\left( {1; - 2} \right),B\left( { - 1; - 1} \right)$

b) +) Thay tọa độ điểm C vào phương trình đường thẳng $\Delta$ ta có: $\left\{ \begin{array}{l}1 = 1 - 2t\\ - 1 =  - 2 + t\end{array} \right.$. Do hệ phương trình vô nghiệm nên C không thuộc đường thẳng $\Delta$

+) Thay tọa độ điểm D vào phương trình đường thẳng $\Delta$ ta có: $\left\{ \begin{array}{l}1 = 1 - 2t\\3 =  - 2 + t\end{array} \right.$. Do hệ phương trình vô nghiệm nên D không thuộc đường thẳng $\Delta$