Giải mục II trang 21, 22, 23, 24 SGK Toán 10 tập 1 - Cánh diều
Cho bất phương trình 2x – y>2 (3). a) Trong mặt phẳng toạ độ Oxy, vẽ đường thẳng d:2x - y = 2 => y = 2x - 2 Biểu diễn miền nghiệm của mỗi bất phương trình sau:
Hoạt động 3
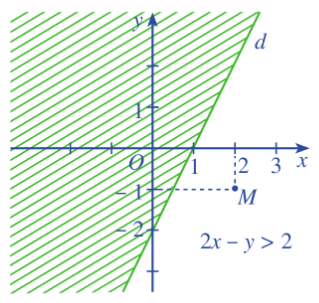
Cho bất phương trình 2x – y > 2 (3).
a) Trong mặt phẳng toạ độ Oxy, vẽ đường thẳng \(d:2x - y = 2 \Leftrightarrow y = 2x - 2\).
b) Xét điểm M(2;-1). Chứng tỏ (2;-1) là nghiệm của bất phương trình (3).
c) Đường thẳng d chia mặt phẳng toạ độ thành hai nửa mặt phẳng. Gạch đi nửa mặt phẳng không chứa điểm M(2;- 1).
Phương pháp giải:
a) Vẽ đường thẳng y = 2x - 2 trên mặt phẳng tọa độ.
b) Thay tọa độ điểm M vào bất phương trình (3), nếu thỏa mãn thì (2;-1) là một nghiệm của bất phương trình (3).
c) Gạch phần không chứa điểm M.
Lời giải chi tiết:
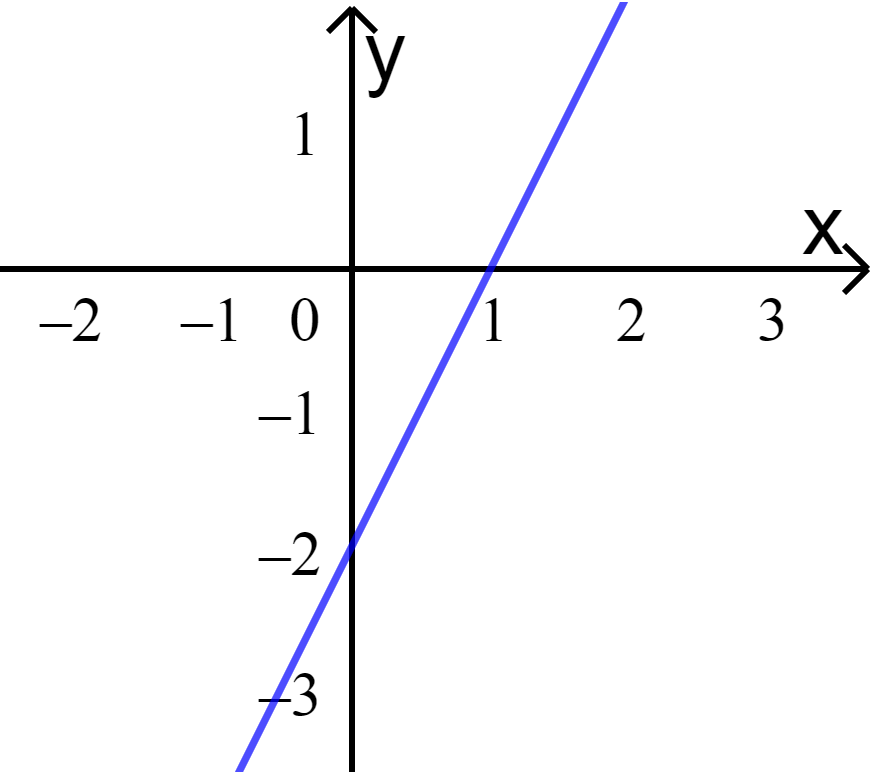
a) Cho x = 0 => y = -2.
Cho y = 0 => x = 1.
Nối hai điểm (0;-2) và (1;0) ta được:
b) Thay tọa độ điểm M vào bất phương trình (3) ta được:
\(2.2 - \left( { - 1} \right) > 2 \Leftrightarrow 5 > 2\)(Luôn đúng)
Vậy (2;-1) là một nghiệm của bất phương trình (3)
c) Ta gạch đi nửa mặt phẳng không chứa M được:
Luyện tập – Vận dụng 2
Biểu diễn miền nghiệm của mỗi bất phương trình sau:
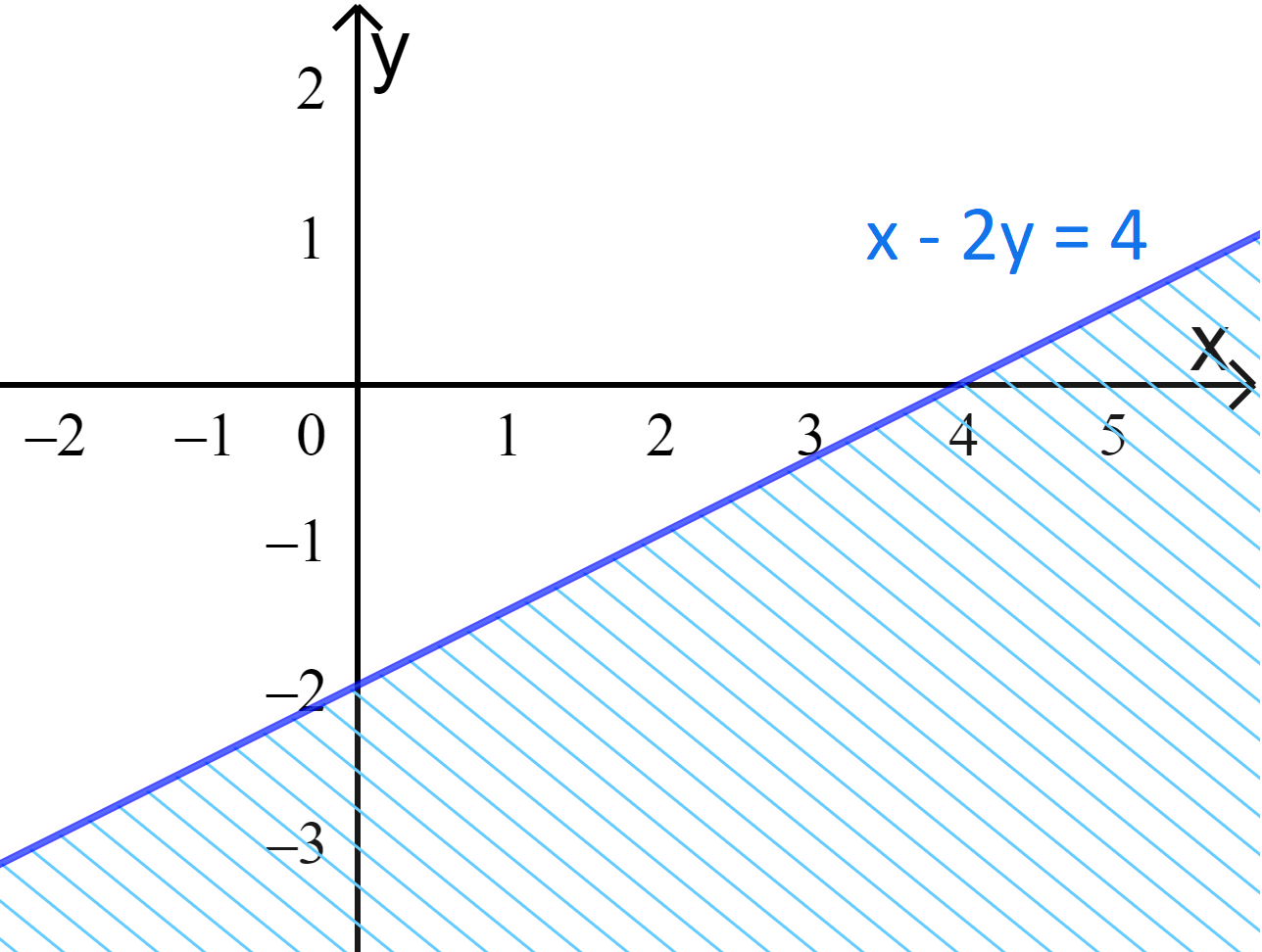
a) \(x - 2y < 4\)
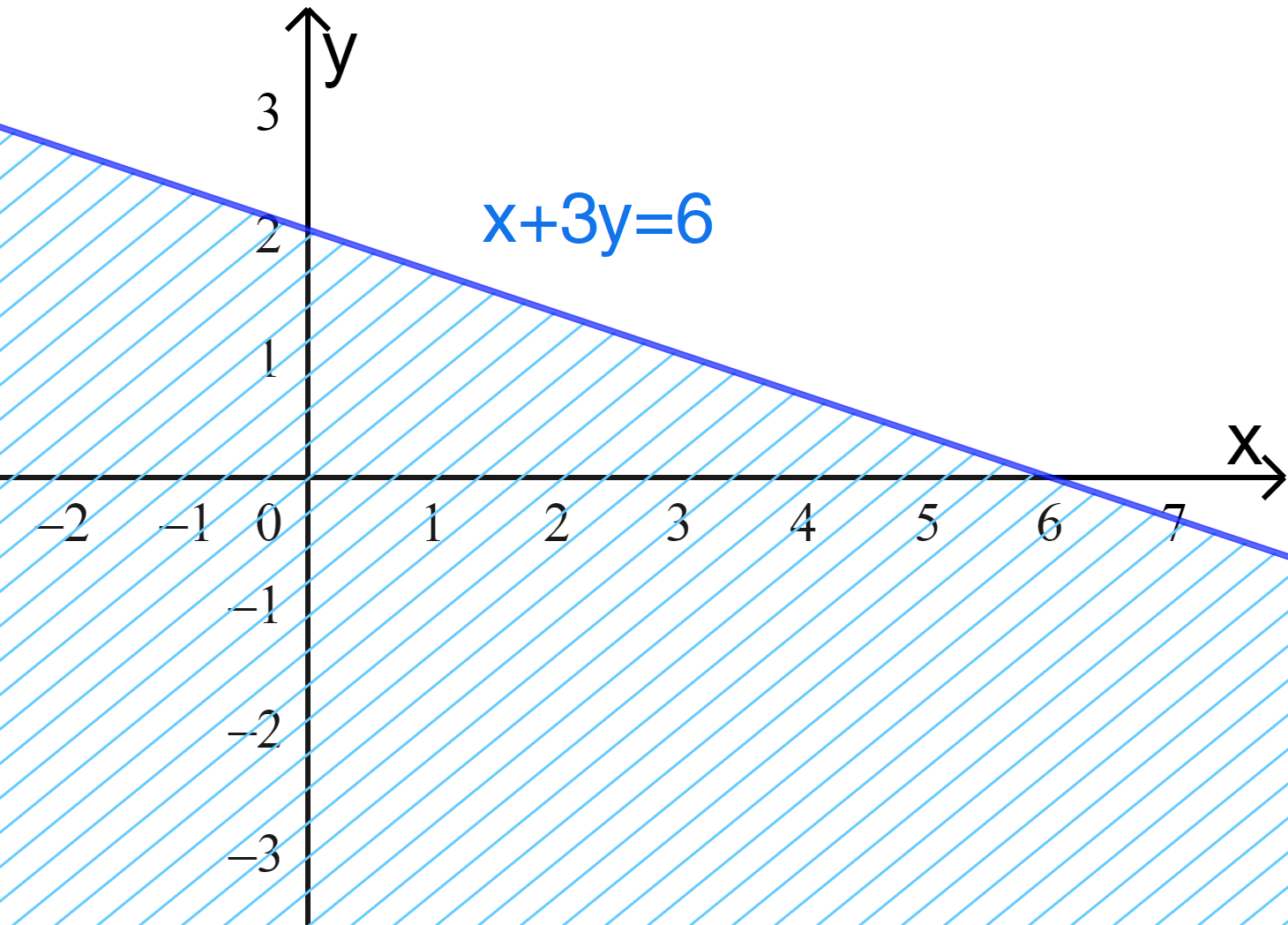
b) \(x + 3y \ge 6\).
Phương pháp giải:
Các bước biểu diễn miền nghiệm:
- Vẽ đường thẳng.
- Thay tọa độ điểm O(0;0) vào bất phương trình.
- Nếu thỏa mãn thì điểm O nằm trong miền nghiệm, ta gạch phần không chứa O.
- Ngược lại thì không nằm trong miền nghiệm ta gạch phần chứa O.
Lời giải chi tiết:
a) Ta vẽ đường thẳng d:\(x - 2y = 4 \Leftrightarrow y = \frac{x}{2} - 2\).
Cho x = 0 thì y = –2, cho y = 0 thì x = 4. Đường thẳng d đi qua 2 điểm (0;–2) và (4;0).
Thay tọa độ điểm O(0;0) vào bất phương trình \(x - 2y < 4\) ta được:
\(0 - 2.0 < 4\) (Luôn đúng).
Vậy O nằm trong miền nghiệm.
Ta có miền nghiệm:
b) Ta vẽ đường thẳng d:\(x+3y=6 \).
Cho x = 0 thì y = 2, cho y = 0 thì x = 6, do đó đường thẳng d đi qua hai điểm (0;2) và (6;0).
Thay tọa độ điểm O(0;0) vào bất phương trình \(x+3y=6 \) ta được:
\(0+3.0 < 6\).
Vậy O không nằm trong miền nghiệm.
Ta có miền nghiệm: