Giải mục III trang 36 SGK Toán 10 tập 1 - Cánh diều
a) So sánh f(-2),f(-1). Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ -2 đến -1. b) So sánh f(1), f(2). Nêu nhận xét về sự biến thiên của giá trị hàm số khị giá trị biến x tăng dần từ 1 đến 2.
Hoạt động 5
Cho hàm số \(f\left( x \right) = x + 1\).
a) So sánh \(f\left( 1 \right)\) và \(f\left( 2 \right)\).
b) Chứng minh rằng nếu \({x_1},{x_2} \in \mathbb{R}\) sao cho \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Phương pháp giải:
a) Tính \(f\left( 1 \right)\) và \(f\left( 2 \right)\) và so sánh .
b) Thay \({x_1},{x_2}\) vào \(f\left( x \right) = x + 1\) tìm \(f\left( {{x_1}} \right),f\left( {{x_2}} \right)\) rồi chứng minh \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Lời giải chi tiết:
a) Ta có:
\(f\left( 1 \right) = 1 + 1 = 2\)
\(f\left( 2 \right) = 2 + 1 = 3\)
\( \Rightarrow f\left( 2 \right) > f\left( 1 \right)\)
b) Ta có:
\(f\left( {{x_1}} \right) = {x_1} + 1;f\left( {{x_2}} \right) = {x_2} + 1\)
\(\begin{array}{l}f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \left( {{x_1} + 1} \right) - \left( {{x_2} + 1} \right)\\ = {x_1} - {x_2} < 0\end{array}\)
Vậy \({x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Luyện tập – vận dụng 6
Chứng tỏ hàm số \(y = 6{x^2}\) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
Phương pháp giải:
Xét hai số bất kì \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\). Chứng minh \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
Lời giải chi tiết:
Xét hai số bất kì \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\).
Ta có: \(f\left( {{x_1}} \right) = 6x_1^2;f\left( {{x_2}} \right) = 6x_2^2\)
\(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = 6x_1^2 - 6x_2^2\)\( = 6\left( {{x_1} - {x_2}} \right)\left( {{x_1} + {x_2}} \right)\)
\({x_1} < {x_2} \Rightarrow {x_1} - {x_2} < 0\)
\({x_1} < 0;{x_2} < 0 \Rightarrow {x_1} + {x_2} < 0\)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0\)
Vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\).
Hoạt động 6
Cho đồ thị hàm số \(y = f\left( x \right) = {x^2}\) như Hình 6 .
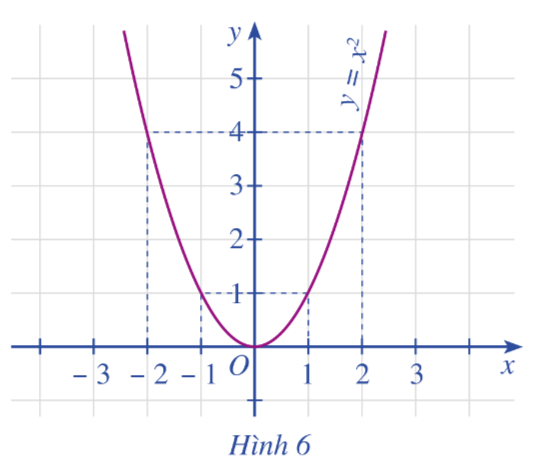
a) So sánh \(f\left( { - 2} \right),f\left( { - 1} \right)\). Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ -2 đến -1.
b) So sánh \(f\left( 1 \right),f\left( 2 \right)\). Nêu nhận xét về sự biến thiên của giá trị hàm số khị giá trị biến x tăng dần từ 1 đến 2.
Phương pháp giải:
a)
- Tính \(f\left( { - 2} \right),f\left( { - 1} \right)\)
- Lấy \({x_1},{x_2} \in \left( { - 2; - 1} \right)\) sao cho \({x_1} < {x_2}\). Chứng minh \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
b)
- Tính \(f\left( 1 \right),f\left( 2 \right)\)
- Lấy \({x_1},{x_2} \in \left( {1;2} \right)\) sao cho \({x_1} < {x_2}\). Chứng minh \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Lời giải chi tiết:
a)
\(f\left( { - 2} \right) = {\left( { - 2} \right)^2} = 4;\)\(f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\( \Rightarrow f\left( { - 2} \right) > f\left( { - 1} \right)\)
Lấy \({x_1},{x_2} \in \left( { - 2; - 1} \right)\) sao cho \({x_1} < {x_2}\).
\( \Rightarrow {x_1} - {x_2} < 0\)
\({x_1},{x_2} < 0 \Rightarrow {x_1} + {x_2} < 0\)
Ta có:
\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) > 0\\ \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\end{array}\)
=> Hàm số nghịch biến trên (-2;-1)
Vậy hàm số giảm khi x tăng từ -2 đến -1
b)
\(\begin{array}{l}f\left( 1 \right) = 1;f\left( 2 \right) = {2^2} = 4\\ \Rightarrow f\left( 1 \right) < f\left( 2 \right)\end{array}\)
Lấy \({x_1},{x_2} \in \left( {1;2} \right)\) sao cho \({x_1} < {x_2}\).
\( \Rightarrow {x_1} - {x_2} < 0\)
\({x_1},{x_2} > 0 \Rightarrow {x_1} + {x_2} > 0\)
Ta có:
\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) < 0\\ \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\end{array}\)
=> Hàm số đồng biến trên (1;2)
Vậy hàm số tăng khi x tăng từ 1 đến 2.