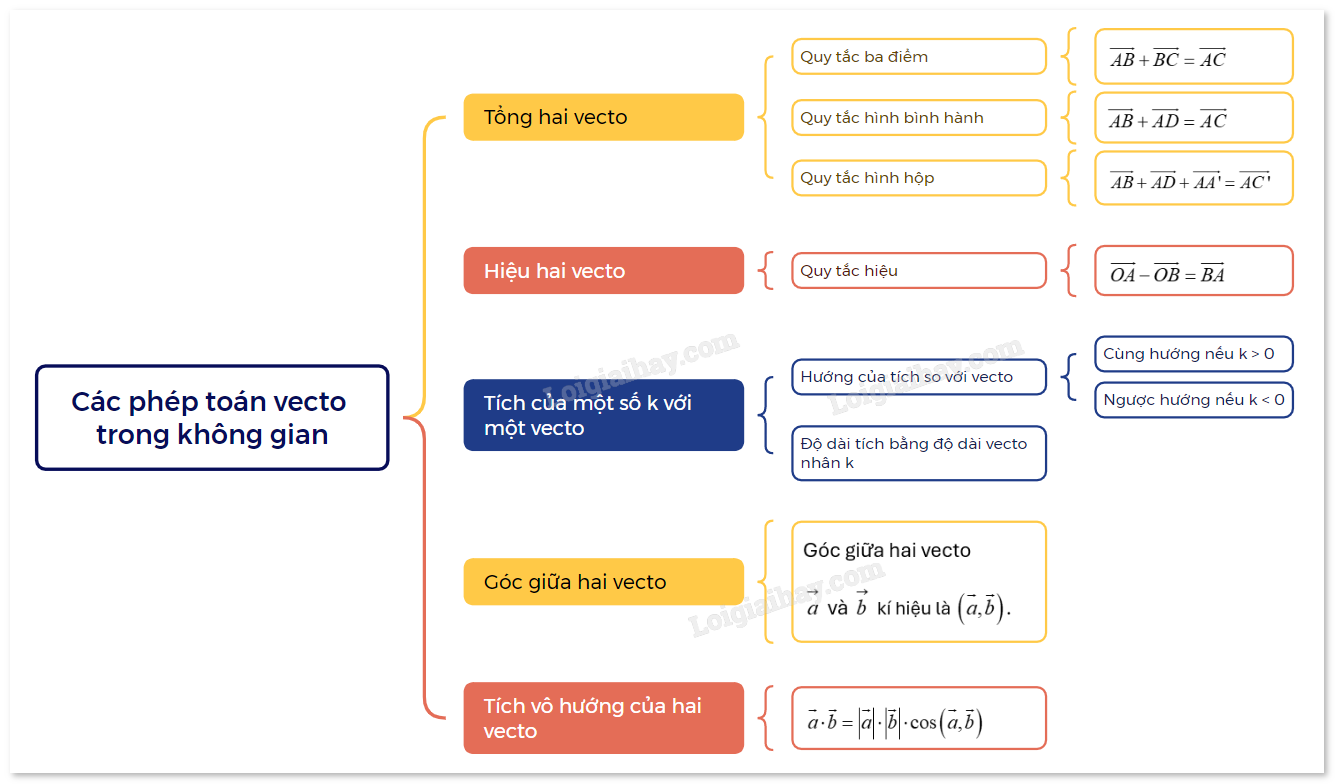
Lý thuyết Các phép toán vecto trong không gian Toán 12 Cùng khám phá
1. Tổng và hiệu của hai vecto trong không gian a) Tổng của hai vecto
1. Tổng và hiệu của hai vecto trong không gian
a) Tổng của hai vecto
|
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Lấy một điểm A bất kì và các điểm B,C sao cho \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Khi đó, vecto \(\overrightarrow {AC} \) được gọi là tổng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu là \(\overrightarrow a + \overrightarrow b \). Phép lấy tổng của hai vecto được gọi là phép cộng vecto. - Với 3 điểm A, B, C trong không gian, ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (Quy tắc 3 điểm). - Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (Quy tắc hình bình hành). - Nếu ABCD.A’B’C’D’ là hình hộp thì \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \) (Quy tắc hình hộp). |
b) Hiệu của hai vecto
|
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Hiệu của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là tổng của hai vecto \(\mathop a\limits^ \to \) và vecto đối của \(\mathop b\limits^ \to \), kí hiệu là \(\mathop a\limits^ \to - \mathop b\limits^ \to \). Phép lấy hiệu của hai vecto được gọi là phép trừ vecto. Với ba điểm O, A, B trong không gian, ta có: \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \) (Quy tắc hiệu). |
2. Tích của một số với một vecto trong không gian
|
Trong không gian, tích của một số thực \(k \ne 0\) với một vecto \(\overrightarrow a \ne \overrightarrow 0 \) là một vecto, kí hiệu là \(k\overrightarrow a \), được xác định như sau: - Cùng hướng với vecto \(\mathop a\limits^ \to \) nếu k > 0; ngược hướng với vecto \(\mathop a\limits^ \to \) nếu k < 0. - Có độ dài bằng \(\left| k \right|.\left| {\overrightarrow a } \right|\). Phép lấy tích của một số với một vecto được gọi là phép nhân một số với một vecto. |
3. Tích vô hướng của hai vecto trong không gian
a) Góc giữa hai vecto trong không gian
| Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Lấy một điểm O bất kỳ và gọi A, B là hai điểm sao cho \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}({0^ \circ } \le \widehat {AOB} \le {180^ \circ })\) được gọi là góc giữa hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu \(\left( {\overrightarrow a ,\overrightarrow b } \right)\). |
b) Tích vô hướng của hai vecto trong không gian
|
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Tích vô hướng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\). |