Lý thuyết Đường tròn Toán 9 Cùng khám phá
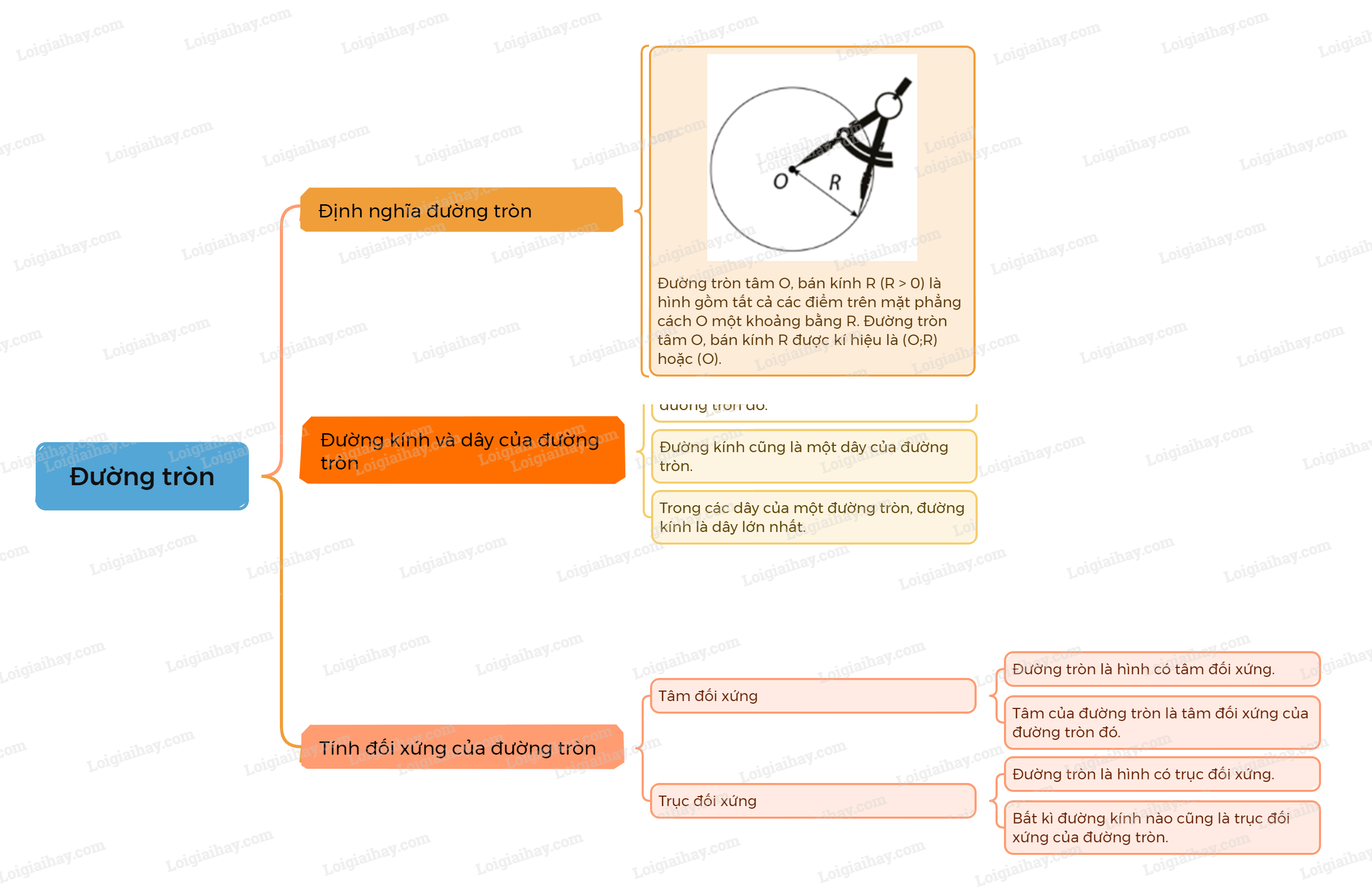
1. Tính đối xứng và trục đối xứng của đường tròn Định nghĩa đường tròn Đường tròn tâm O, bán kính R (R > 0) là hình gồm tất cả các điểm trên mặt phẳng cách O một khoảng bằng R. Đường tròn tâm O, bán kính R được kí hiệu là (O;R) hoặc (O).
1 . Tính đối xứng và trục đối xứng của đường tròn
Định nghĩa đường tròn
|
Đường tròn tâm O, bán kính R (R > 0) là hình gồm tất cả các điểm trên mặt phẳng cách O một khoảng bằng R. Đường tròn tâm O, bán kính R được kí hiệu là (O;R) hoặc (O). |
Tâm đối xứng của đường tròn
|
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó. |
Trục đối xứng của đường tròn
|
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn. |
2. Đường kính và dây của đường tròn
Đoạn thẳng nối hai điểm phân biệt của đường tròn được gọi là một dây của đường tròn đó.
Lưu ý: Đường kính cũng là một dây của đường tròn.
Ví dụ:
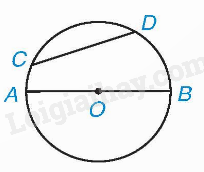
Trong hình trên, CD là một dây, AB là một đường kính của (O).
Mối liên hệ giữa độ dài đường kính và độ dài dây của một đường tròn
|
Trong các dây của một đường tròn, đường kính là dây lớn nhất. |