Lý thuyết Vị trí tương đối của hai đường tròn Toán 9 Cùng khám phá
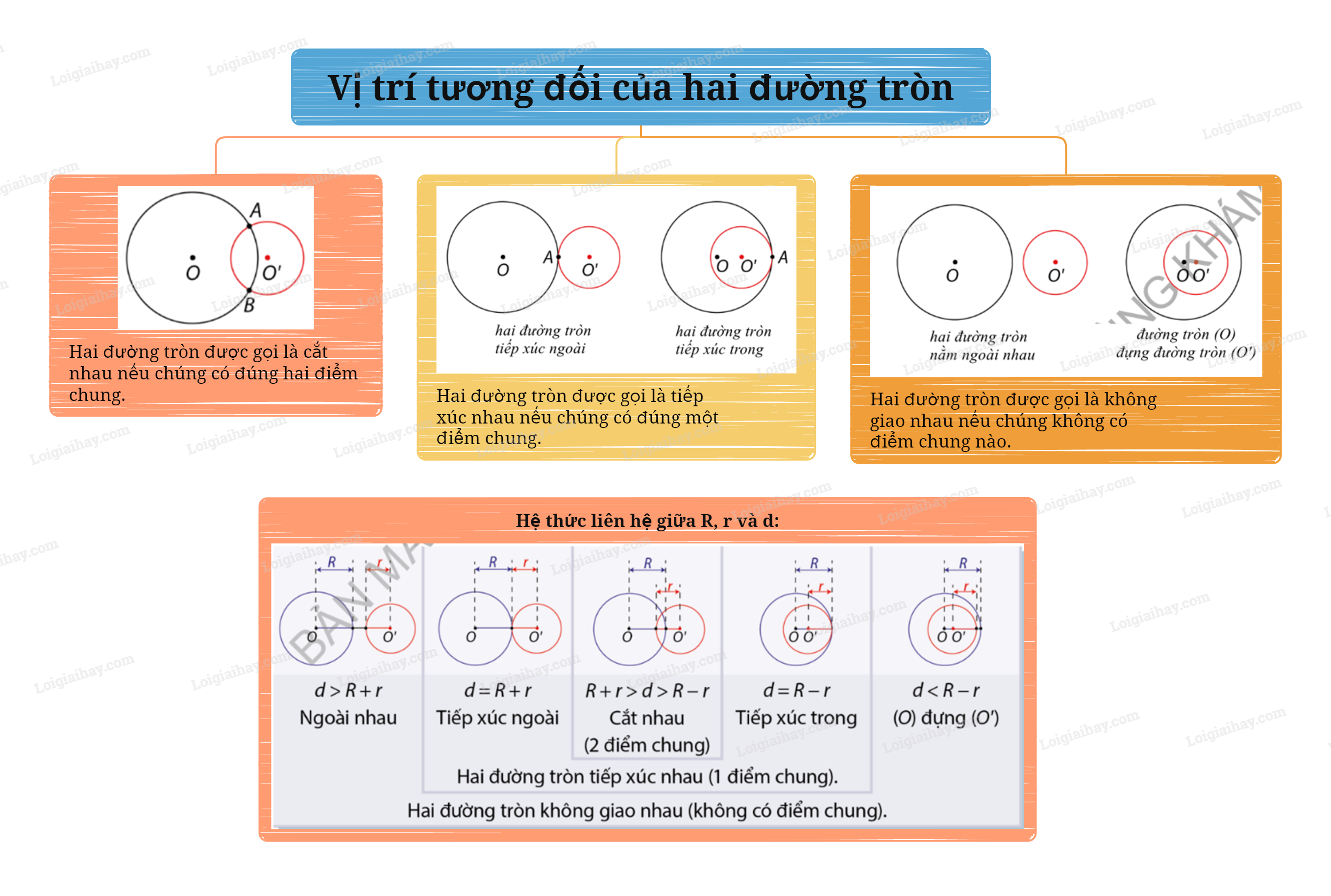
Hai đường tròn được gọi là cắt nhau nếu chúng có đúng hai điểm chung. Hai đường tròn được gọi là tiếp xúc nhau nếu chúng có đúng một điểm chung. Hai đường tròn được gọi là không giao nhau nếu chúng không có điểm chung nào.
|
Hai đường tròn được gọi là cắt nhau nếu chúng có đúng hai điểm chung. Hai đường tròn được gọi là tiếp xúc nhau nếu chúng có đúng một điểm chung. Hai đường tròn được gọi là không giao nhau nếu chúng không có điểm chung nào. |
Lưu ý:
- Điểm chung của hai đường tròn cắt nhau được gọi là giao điểm . Điểm chung của hai đường tròn tiếp xúc nhau được gọi là tiếp điểm.
- Nếu hai đường tròn tiếp xúc nhau và một đường tròn nằm trong đường tròn còn lại thì hai đường tròn gọi là tiếp xúc trong, ngược lại ta nói hai đường tròn tiếp xúc ngoài .
Ví dụ 1:
Hai đường tròn cắt nhau:
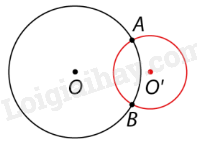
Hai đường tròn tiếp xúc nhau:
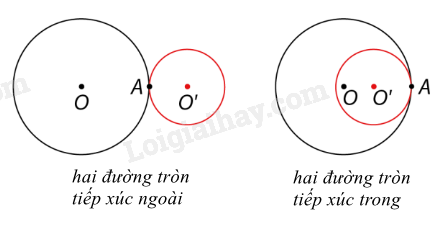
Hai đường tròn không giao nhau:
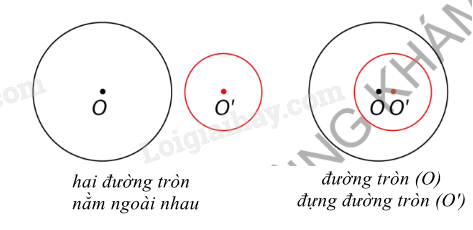
Ví dụ 2:
- Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì:
4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm.
- Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm.
- Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm.
- Cho đường tròn (O;3cm) và (O’;4cm) có \(OO' > 8cm\) thì \(OO' = 8cm > 3cm + 4cm = R + R'\) nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau.
Hệ thức liên hệ giữa R, r và d: