Lý thuyết Tứ giác nội tiếp Toán 9 Cùng khám phá
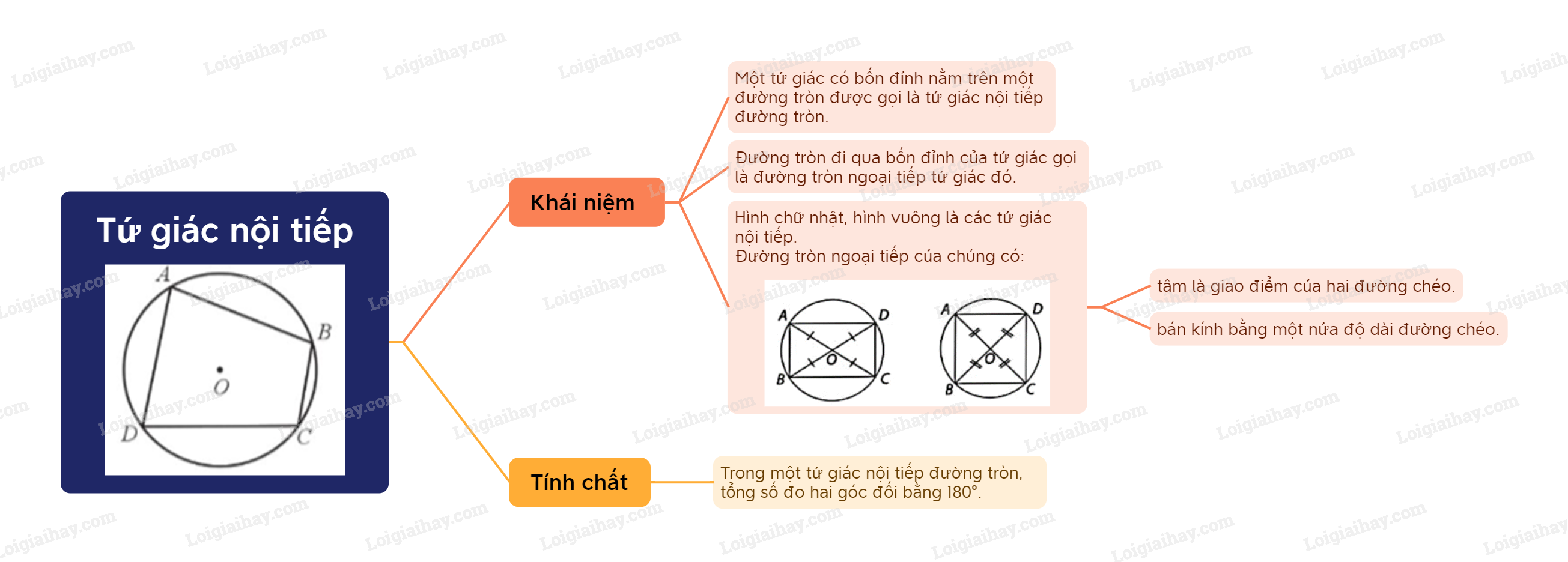
1. Khái niệm tứ giác nội tiếp - Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn. - Đường tròn đi qua bốn đỉnh của tứ giác gọi là đường tròn ngoại tiếp tứ giác đó.
1. Khái niệm tứ giác nội tiếp
|
- Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn . - Đường tròn đi qua bốn đỉnh của tứ giác gọi là đường tròn ngoại tiếp tứ giác đó. |
Ví dụ:
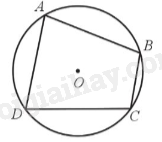
Tứ giác ABCD là tứ giác nội tiếp và đường tròn (O) được gọi là đường tròn ngoại tiếp tứ giác ABCD.
|
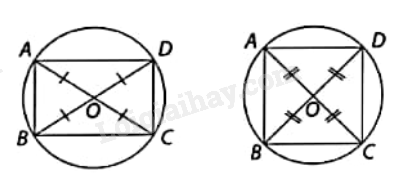
Hình chữ nhật, hình vuông là các tứ giác nội tiếp. Đường tròn ngoại tiếp của hình chữ nhật và hình vuông có tâm là giao điểm của hai đường chéo và bán kính là nửa đường chéo.
|
Ví dụ:
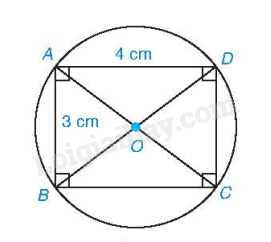
Áp dụng định lí Pythagore cho tam giác ABD vuông tại A, ta có:
\(B{D^2} = A{B^2} + A{D^2} = {3^2} + {4^2} = 25\) nên \(BD = 5cm\).
Do đó, ta có \(R = \frac{{BD}}{2} = 2,5cm\).
Đường tròn (O;2,5) là đường tròn ngoại tiếp hình chữ nhật ABCD.
2. Tính chất
|
Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc đối bằng \(180^\circ \). |
Ví dụ:
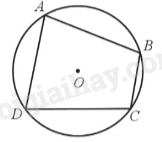
Tứ giác ABCD nội tiếp (O) nên \(\widehat A + \widehat C = 180^\circ ;\widehat B + \widehat D = 180^\circ \).