Lý thuyết Hai đường thẳng song song - SGK Toán 11 Kết nối tri thức — Không quảng cáo

1. Vị trí tương đối của hai đường thẳng

Cho hai đường thẳng a, b trong không gian.

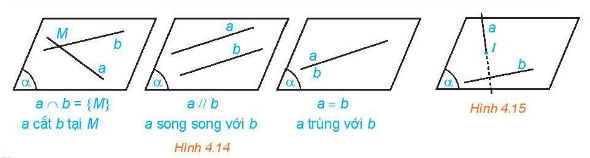
• Nếu a và b cùng nằm trong một mặt phẳng thì ta nói a và b đồng phẳng. Khi đó, a và b có thể cắt nhau, song song với nhau hoặc trùng nhau.
• Nếu a và b không cùng nằm trong bất kì mặt phẳng nào thì ta nói a và b chéo nhau. Khi đó, ta cũng nói a chéo với b hoặc b chéo với a.

2. Tính chất của hai đường thẳng song song

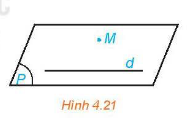
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.

Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì song song với nhau.

Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì 3 giao tuyến đó đồng quy hoặc đôi một song song.

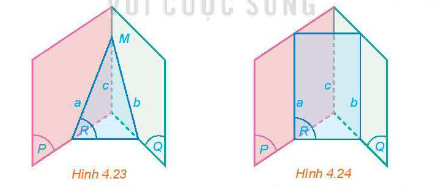
* Chú ý: Nếu hai mặt phẳng chứa 2 đường thẳng song song với nhau thì giao tuyến (nếu có) của chúng song song với 2 đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

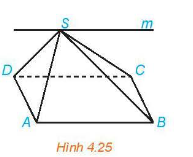
VD: \(\left( {SAB} \right) \cap \left( {SBC} \right) = Sm\)