Lý thuyết Khoảng cách - Toán 11 Kết nối tri thức
1. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng
1. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng
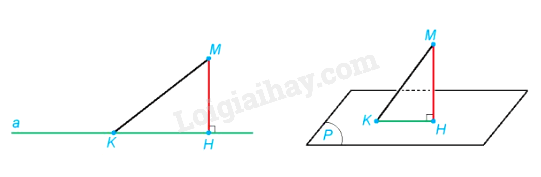
- Khoảng cách từ một điểm M đến một đường thẳng a, kí hiệu là d(M, a), là khoảng cách giữa M và hình chiếu H của M trên a.
- Khoảng cách từ một điểm M đến một mặt phẳng (P), kí hiệu d(M, (P)), là khoảng cách giữa M và hình chiếu H của M trên (P).
Chú ý: d(M, a) = 0 khi và chỉ khi \(M \in a;d\left( {M,\left( P \right)} \right) = 0\) khi và chỉ khi \(M \in \left( P \right)\).
Nhận xét: Khoảng cách từ M đến đường thẳng a (mặt phẳng (P)) là khoảng cách nhỏ nhất giữa M và một điểm thuộc a (thuộc (P)).
Chú ý: Khoảng cách từ đỉnh đến mặt phẳng chứa mặt đáy của một hình chóp được gọi là chiều cao của hình chóp đó.
2. Khoảng cách giữa các đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song
- Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a, kí hiệu d(a, (P)), là khoảng cách từ một điểm bất kì trên a đến (P).
- Khoảng cách giữa hai mặt phẳng song song (P) và (Q), kí hiệu d((P), (Q)), là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia.
- Khoảng cách giữa hai đường thẳng song song m và n, kí hiệu d(m, n), là khoảng cách từ một điểm thuộc đường thẳng này đến đường thẳng kia.
Chú ý: Khoảng cách giữa hai đáy của một hình lăng trụ được gọi là chiều cao của hình lăng trụ đó.
3. Khoảng cách giữa hai đường thẳng chéo nhau
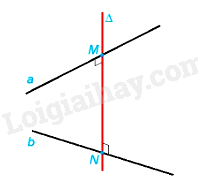
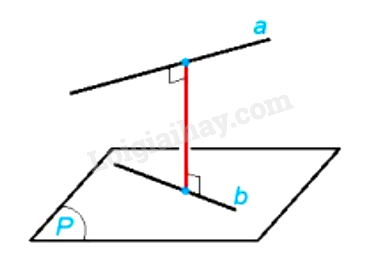
Đường thẳng \(\Delta \) cắt hai đường thẳng chéo nhau a, b và vuông góc với cả hai đường thẳng đó được gọi là đường vuông góc chung của a và b.
Nếu đường vuông góc chung \(\Delta \) cắt a, b tương ứng tại M, N thì độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a, b.
Nhận xét:
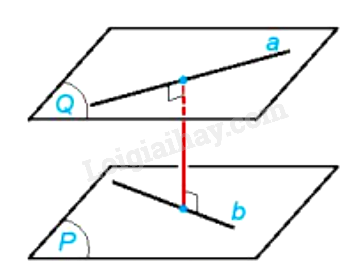
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song, tương ứng chứa hai đường thẳng đó.