Lý thuyết Hàm số liên tục - SGK Toán 11 Cùng khám phá — Không quảng cáo

I. Hàm số liên tục tại một điểm và liên tục trên một khoảng

1. Hàm số liên tục tại 1 điểm

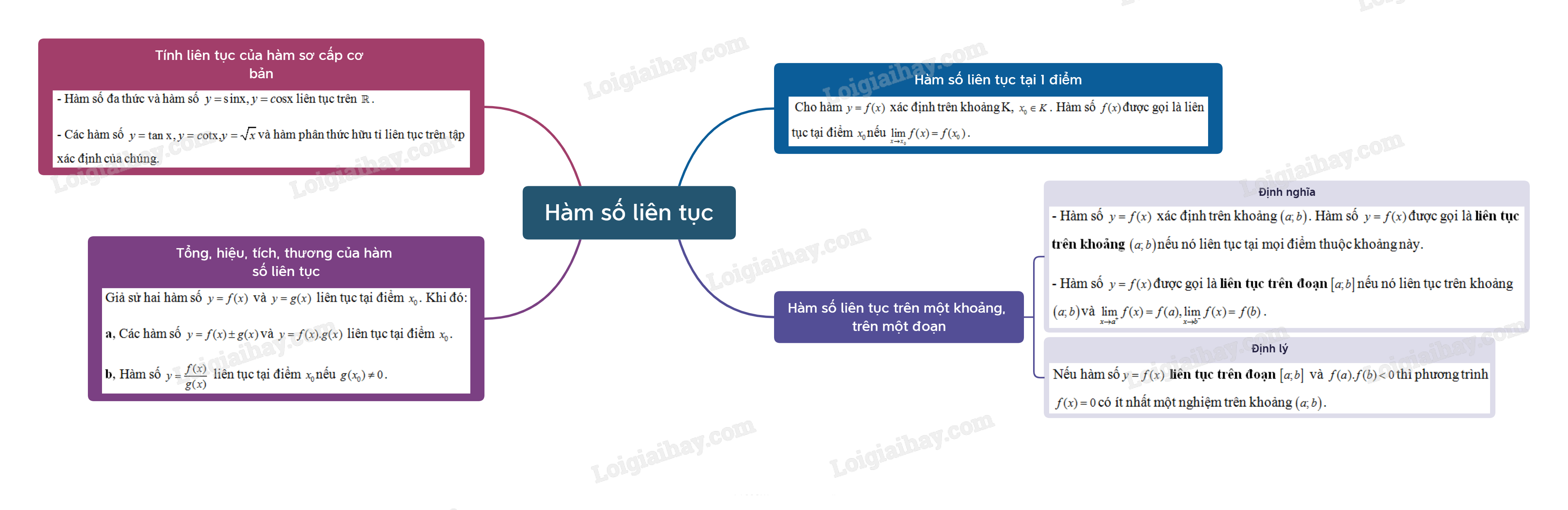
Cho hàm $y = f(x)$ xác định trên khoảng K, ${x_0} \in K$. Hàm số $f(x)$ được gọi là liên tục tại điểm ${x_0}$ nếu $\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})$.

Hàm số không liên tục tại ${x_0}$ được gọi là gián đoạn tại điểm đó.

2. Hàm số liên tục trên một khoảng

- Hàm số $y = f(x)$ xác định trên khoảng $\left( {a;b} \right)$

Hàm số $y = f(x)$ được gọi là liên tục trên khoảng $\left( {a;b} \right)$ nếu nó liên tục tại mọi điểm thuộc khoảng này.

- Hàm số $y = f(x)$ được gọi là liên tục trên đoạn $\left[ {a;b} \right]$ nếu nó liên tục trên khoảng $\left( {a;b} \right)$ và $\mathop {\lim }\limits_{x \to {a^ + }} f(x) = f(a),\mathop {\lim }\limits_{x \to {b^ - }} f(x) = f(b)$.

* Nhận xét:

- Đồ thị hàm số liên tục trên một khoảng, đoạn là “đường liền” trên khoảng, đoạn  đó.

- Nếu hàm số$y = f(x)$ liên tục trên đoạn $\left[ {a;b} \right]$ và $f(a).f(b) < 0$thì phương trình $f(x) = 0$có ít nhất một nghiệm trên khoảng $\left( {a;b} \right)$.

II. Một số định lí cơ bản

1. Định lí 1

- Hàm số đa thức và hàm số $y = {\mathop{\rm s}\nolimits} {\rm{inx}},y = c{\rm{osx}}$liên tục trên $\mathbb{R}$.

- Các hàm số $y = \tan {\rm{x}},y = c{\rm{otx,}}y = \sqrt x$ và hàm phân thức hữu tỉ (thương của hai đa thức) liên tục trên tập xác định của chúng.

2. Định lí 2

Giả sử hai hàm số $y = f(x)$ và $y = g(x)$ liên tục tại điểm ${x_0}$. Khi đó:

a, Các hàm số $y = f(x) \pm g(x)$ và $y = f(x).g(x)$ liên tục tại điểm ${x_0}$.

b, Hàm số $y = \frac{{f(x)}}{{g(x)}}$ liên tục tại điểm ${x_0}$ nếu $g({x_0}) \ne 0$.

c, Hàm số $y = f(x)$ liên tục trên khoảng K và $f(x) \ge 0,\forall x \in K$. Khi đó hàm số $y = \sqrt {f(x)}$ liên tục trên K.