Lý thuyết Lũy thừa của một số hữu tỉ SGK Toán 7 - Chân trời sáng tạo
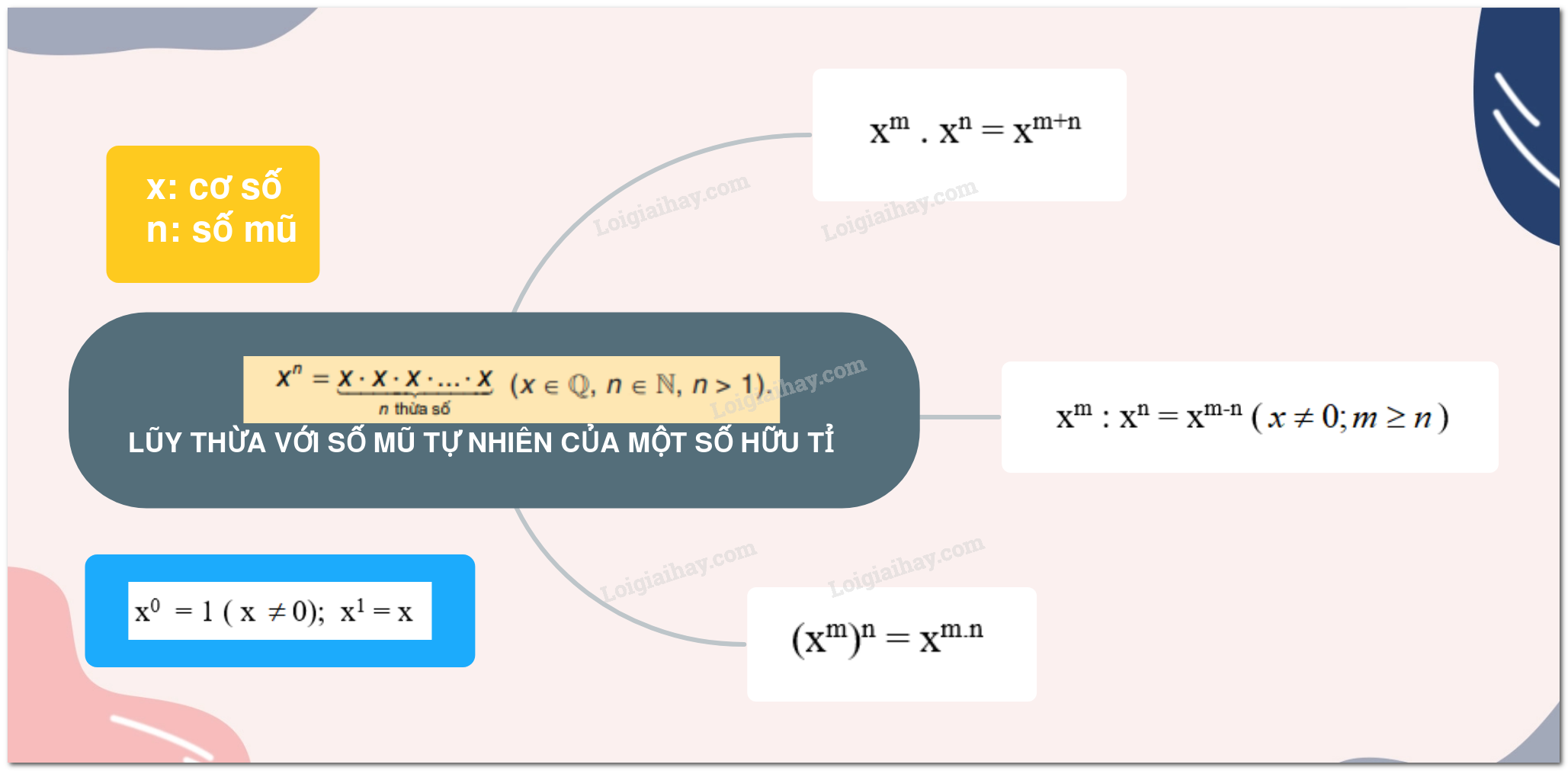
1. Lũy thừa với số mũ tự nhiên
1. Lũy thừa với số mũ tự nhiên
Lũy thừa bậc n của một số hữu tỉ x , kí hiệu x n , là tích của n thừa số x ( n là số tự nhiên lớn hợn 1)
![]()
x n đọc là x mũ n hoặc x lũy thừa n hoặc lũy thừa bậc n của x.
x: cơ số
n: số mũ
Quy ước: x 0 = 1 ( x \( \ne \)0); x 1 = x
Chú ý:
\(\begin{array}{l}{(x.y)^n} = {x^n}.{y^n}\\{(\frac{x}{y})^n} = \frac{{{x^n}}}{{{y^n}}}\end{array}\)
+ Lũy thừa số mũ chẵn của 1 số hữu tỉ luôn dương
+ Lũy thừa số mũ lẻ của 1 số hữu tỉ âm luôn âm
+ Lũy thừa số mũ chẵn của 1 số hữu tỉ dương luôn dương
2. Tích và thương hai lũy thừa cùng cơ số
+ Khi nhân 2 lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng 2 số mũ
x m . x n = x m+n
+ Khi chia 2 lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi lũy thừa của số chia
x m : x n = x m-n (\(x \ne 0;m \ge n\))
Ví dụ: 7 4 . 7 8 = 7 4+8 = 7 12
7 5 : (-7) 2 = 7 5 : 7 2 = 7 5-2 = 7 3
3. Lũy thừa của lũy thừa
Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ.
(x m ) n = x m.n
Ví dụ: [(-3) 3 ] 4 = (-3) 3.4 = (-3) 12
4. Mở rộng
Lũy thừa với số mũ nguyên âm của một số hữu tỉ
\(x^{-n} = \frac{1}{x^n} (x \ne 0) \)
Ví dụ: \(3^{-2} = \frac{1}{3^2}\)