Lý thuyết Số vô tỉ. Căn bậc hai số học SGK Toán 7 Chân trời sáng tạo — Không quảng cáo

1. Biểu diễn thập phân của một số hữu tỉ

Ví dụ: Các số thập phân đã học như -4,3 ; 0,35;… còn được gọi là số thập phân hữu hạn.

Các số -0,2(7) ; 1,3(18) ; 5,(1) ;…. là những số thập phân vô hạn tuần hoàn với chu kì lần lượt là 7 ; 18 ; 1.

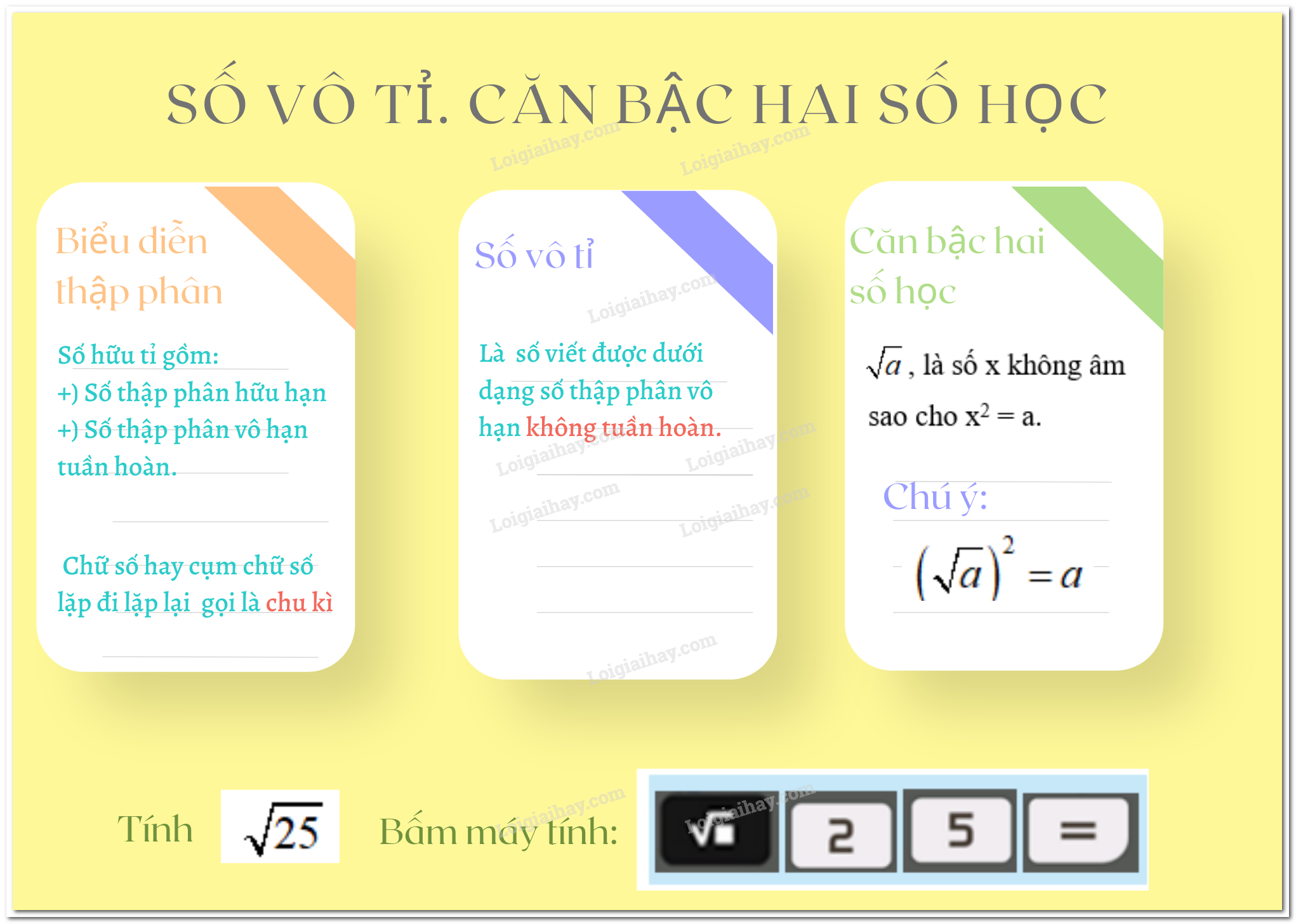
+ Mỗi số thập phân vô hạn tuần hoàn biểu diễn 1 số hữu tỉ. Chữ số hay cụm chữ số lặp đi lặp lại được gọi là chu kì.

Chú ý:

+ Mọi số hữu tỉ đều viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.

+ Nếu phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố nào khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.

Ví dụ: $\frac{3}{{80}} = \frac{3}{{{2^4}.5}} = \frac{{{{3.5}^3}}}{{{2^4}{{.5.5}^3}}} = \frac{{375}}{{10000}} = 0,0375$

+ Nếu phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn.

Ví dụ: $\frac{7}{{30}} = 0,2333.... = 0,2(3)$

2. Số vô tỉ

Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.

Ví dụ: $\pi  = 3,1415926.....;e = 2,71828.....;....$là những sô vô tỉ

Tập hợp các số vô tỉ được kí hiệu là I

3. Căn bậc hai số học

Căn bậc hai số học của một số a không âm, kí hiệu $\sqrt a$, là số x không âm sao cho x ² = a.

Ví dụ: $\sqrt {121}  = 11$ vì 11 > 0 và 11 ² = 121

Chú ý: Cho $a \ge 0$. Khi đó:

+ Đẳng thức $\sqrt a  = b$ đúng nếu $b \ge 0;{b^2} = a$

+ ${\left( {\sqrt a } \right)^2} = a$

4. Tính căn bậc hai số học bằng máy tính cầm tay

Ví dụ: Tính $\sqrt {25}$

Ta bấm liên tiếp các nút: