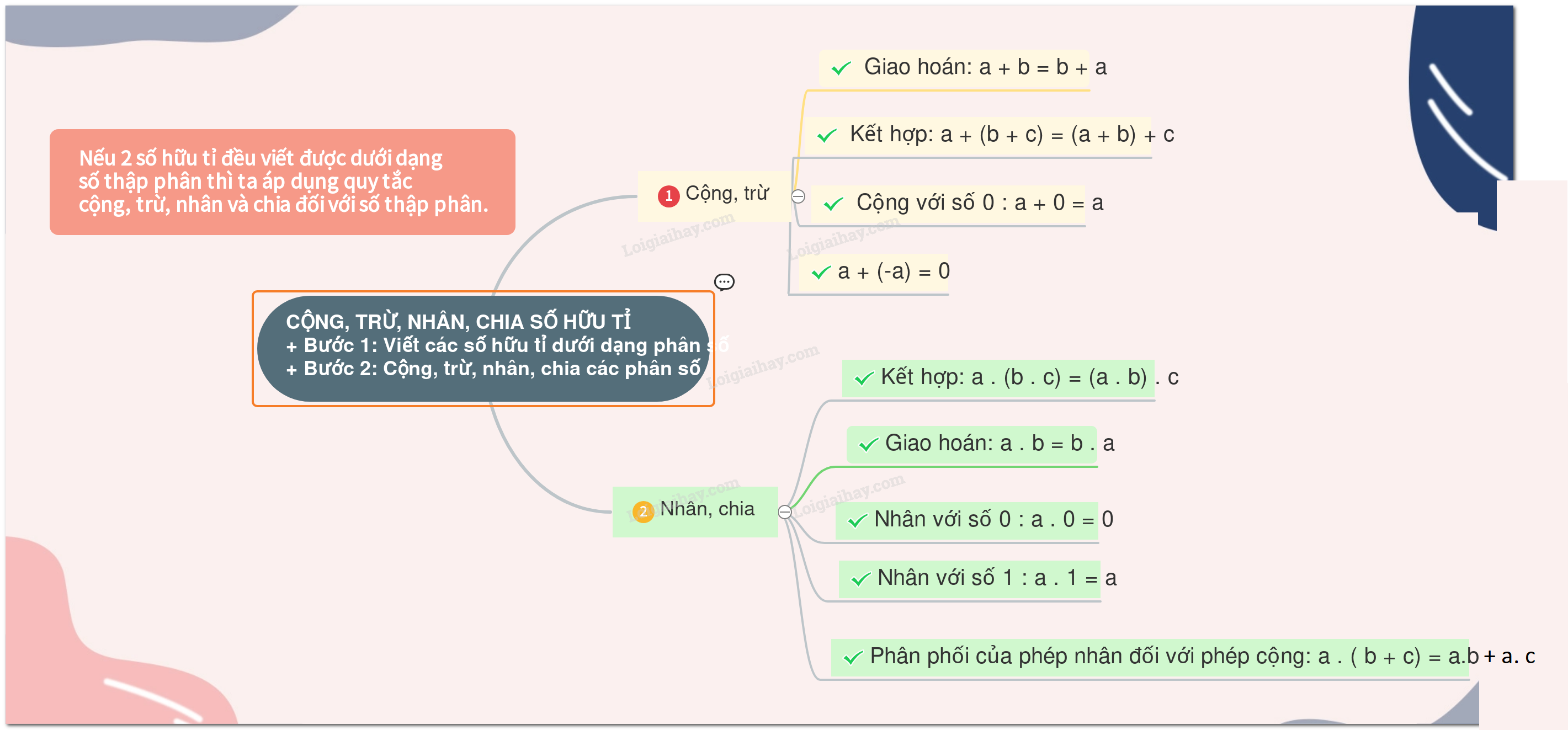
Lý thuyết Tập hợp các số hữu tỉ SGK Toán 7 Chân trời sáng tạo
1. Số hữu tỉ
1. S ố hữu tỉ
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}(a,b \in \mathbb{Z};b \ne 0)\)
Tập hợp các số hữu tỉ được kí hiệu là Q
Ví dụ: \( - 7,21;\frac{{ - 7}}{{ - 9}};\frac{0}{{ - 2}};2\frac{3}{8};...\) là các số hữu tỉ
Chú ý :
+ Các số thập phân đã biết đều là các số hữu tỉ. Các số nguyên, hỗn số cũng là các số hữu tỉ
+ Các phân số bằng nhau là các cách viết khác nhau của cùng một số hữu tỉ
Ví dụ: - \(\frac{9}{{30}}\)= \(\frac{{ - 3}}{{10}}\) nên 2 phân số - \(\frac{9}{{30}}\) và \(\frac{{ - 3}}{{10}}\) cùng biểu diễn 1 số hữu tỉ
2. So sánh hai số hữu tỉ
+ Ta có thể so sánh hai số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh 2 phân số đó.
+ Với 2 số hữu tỉ a và b bất kì, ta luôn có hoặc a = b, hoặc a < b, hoặc a > b
+ Cho 3 số hữu tỉ a, b, c. Nếu a < b; b < c thì a < c ( Tính chất bắc cầu)
+ Trên trục số, nếu a < b thì điểm a nằm trước điểm b
+ Các số hữu tỉ lớn hơn 0 gọi là các số hữu tỉ dương.
+ Các số hữu tỉ nhỏ hơn 0 gọi là các số hữu tỉ âm.
+ Số 0 không là số hữu tỉ âm, cũng không là số hữu tỉ dương.
Chú ý: Trên trục số, các điểm nằm trước gốc O biểu diễn số hữu tỉ âm; các điểm nằm sau gốc O biểu diễn số hữu tỉ dương.
* Cách so sánh hai số hữu tỉ:
Ta viết chúng về cùng dạng phân số (hoặc dạng số thập phân) rồi so sánh chúng.
3. Biểu diễn số hữu tỉ trên trục số
Ta có thể biểu diễn mọi số hữu tỉ trên trục số
Trên trục số, điểm biểu diễn số hữu tỉ a được gọi là điểm a.
Ta chọn phân số tối giản để biểu diễn số hữu tỉ.
4. Số đối của một số hữu tỉ
+ Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ \(\frac{a}{b}\) là số hữu tỉ -\(\frac{a}{b}\)
Trên trục số, điểm biểu diễn số hữu tỉ a được gọi là điểm a.
Trên trục số, 2 điểm biểu diễn 2 số hữu tỉ đối nhau a và –a nằm về 2 phía khác nhau so với điểm O và có cùng khoảng cách đến O.
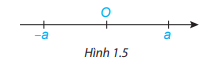
Ví dụ: -5 là số đối của 5