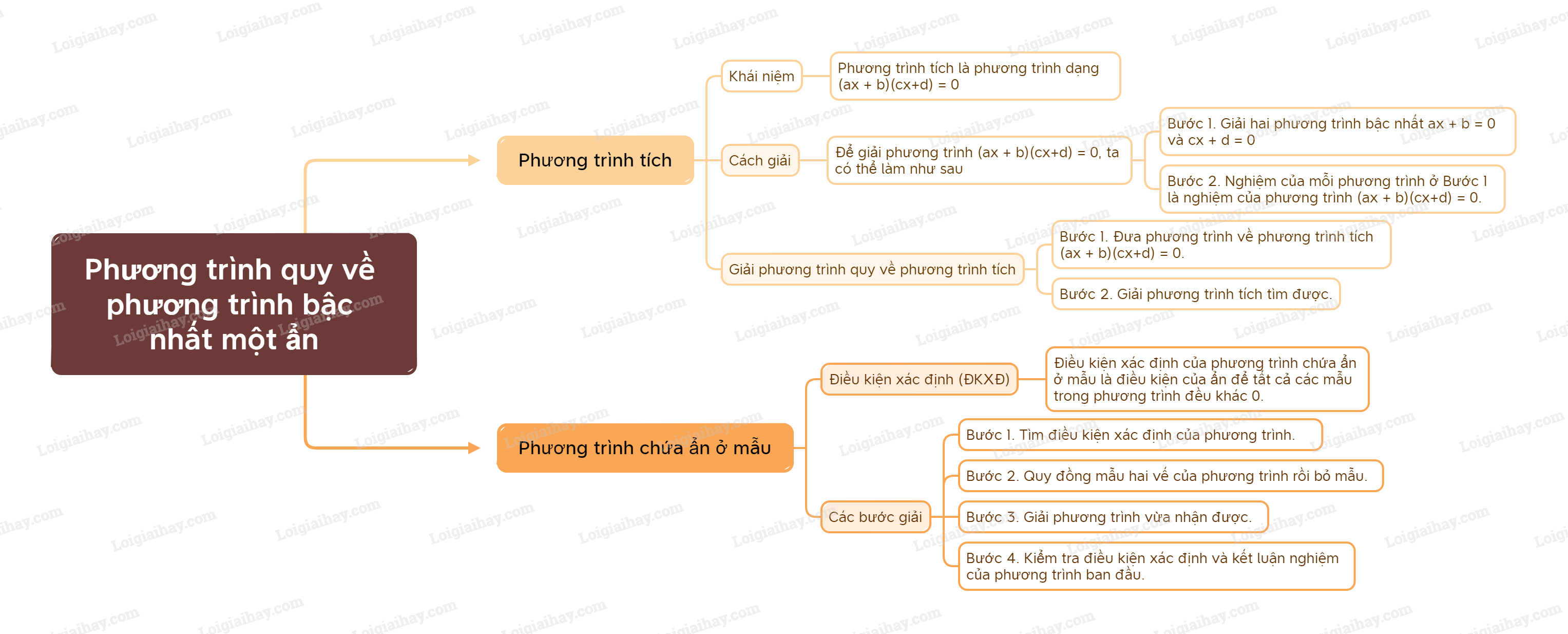
Lý thuyết Phương trình quy về phương trình bậc nhất một ẩn Toán 9 Cùng khám phá
1. Phương trình tích có dạng (left( {ax + b} right)left( {cx + d} right) = 0left( {a ne 0,c ne 0} right)) Cách giải phương trình tích
1. Phương trình tích có dạng \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\left( {a \ne 0,c \ne 0} \right)\)
Cách giải phương trình tích
|
Để giải phương trình tích \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\) với \(a \ne 0\) và \(c \ne 0\), ta có thể làm như sau: Bước 1. Giải hai phương trình \(ax + b = 0\) và \(cx + d = 0\) Bước 2. Nghiệm của mỗi phương trình ở Bước 1 là nghiệm của phương trình \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\). |
Ví dụ 1: Giải phương trình \(\left( {2x + 1} \right)\left( {3x - 1} \right) = 0\)
Lời giải:
Để giải phương trình \(\left( {2x + 1} \right)\left( {3x - 1} \right) = 0\), ta giải hai phương trình sau:
*) \(2x + 1 = 0\)
\(2x = - 1\)
\(x = - \frac{1}{2}\).
*) \(3x - 1 = 0\)
\(3x = 1\)
\(x = \frac{1}{3}\).
Vậy phương trình đã cho có hai nghiệm là \(x = - \frac{1}{2}\) và \(x = \frac{1}{3}\).
Ví dụ 2: Giải phương trình \({x^2} - x = - 2x + 2\).
Lời giải:
Biến đổi phương trình đã cho về phương trình tích như sau:
\(\begin{array}{l}{x^2} - x = - 2x + 2\\{x^2} - x + 2x - 2 = 0\\x\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0\\\left( {x + 2} \right)\left( {x - 1} \right) = 0.\end{array}\)
Ta giải hai phương trình sau:
*) \(x + 2 = 0\)
\(x = - 2\).
*) \(x - 1 = 0\)
\(x = 1\).
Vậy phương trình đã cho có hai nghiệm là \(x = - 2\) và \(x = 1\).
2. Phương trình chứa ẩn ở mẫu
Điều kiện xác định của phương trình chứa ẩn ở mẫu
|
Điều kiện xác định của phương trình chứa ẩn ở mẫu là điều kiện của ẩn để tất cả các mẫu trong phương trình đều khác 0. |
Ví dụ:
- Phương trình \(\frac{{5x + 2}}{{x - 1}} = 0\) có điều kiện xác định là \(x - 1 \ne 0\) hay \(x \ne 1\).
- Phương trình \(\frac{1}{{x + 1}} = 1 + \frac{1}{{x - 2}}\) có điều kiện xác định là \(x + 1 \ne 0\) và \(x - 2 \ne 0\) hay \(x \ne - 1\) và \(x \ne 2\).
Các bước giải phương trình chứa ẩn ở mẫu
|
Bước 1. Tìm điều kiện xác định của phương trình. Bước 2. Quy đồng mẫu hai vế của phương trình rồi bỏ mẫu. Bước 3. Giải phương trình vừa nhận được. Bước 4. Kiểm tra điều kiện xác định và kết luận nghiệm của phương trình ban đầu. |
Ví dụ: Giải phương trình \(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)
Lời giải:
Điều kiện xác định \(x \ne - 1\) và \(x \ne 2\).
\(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)
\(\frac{{2\left( {x - 2} \right) + \left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)
\(2\left( {x - 2} \right) + \left( {x + 1} \right) = 3\).
\(\begin{array}{l}2\left( {x - 2} \right) + \left( {x + 1} \right) = 3\\2x - 4 + x + 1 = 3\\3x - 3 = 3\\3x = 6\\x = 2\end{array}\)
Ta thấy \(x = 2\) không thỏa mãn điều kiện xác định của phương trình.
Vậy phương trình \(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\) vô nghiệm.